一元函数积分学

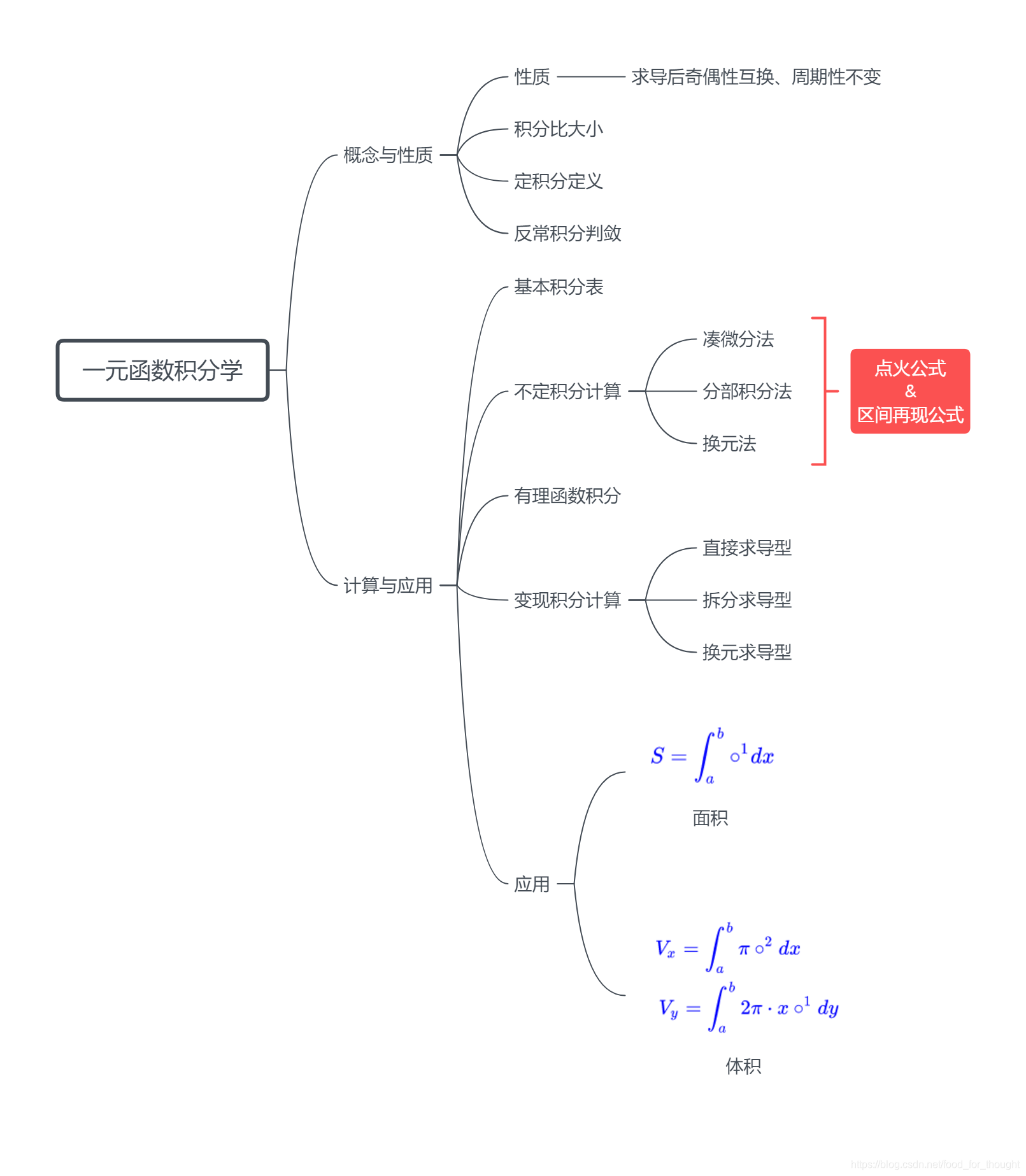
概念与性质

祖孙三代求导后奇偶性互换、周期性不变

$$\begin{array}{rl}[例]& f(x)二阶可导，T=2，奇函数，且f(\frac{1}{2})>0,f^{\prime }(x)>0,比较f(-\frac{1}{2}),f^{\prime }(\frac{3}{2}),f^{\prime \prime }(0)的大小\\ & \because 该函数为奇函数\therefore f(-x)=-f(x)\to f(-\frac{1}{2})=-f(\frac{1}{2})<0\\ & \because f(x):T=2\therefore f^{\prime }(x):T=2且f^{\prime }(x)为偶函数\\ & \therefore f^{\prime }(\frac{3}{2})=f^{\prime }(\frac{3}{2}-2)=f^{\prime }(-\frac{1}{2})=f^{\prime }(\frac{1}{2})>0\\ & \therefore f^{\prime \prime }(x)为奇函数即:f^{\prime \prime }(0)=0\\ & 得f(-\frac{1}{2})<f^{\prime \prime }(0)<f^{\prime }(\frac{3}{2})\end{array}$$

1.前提： 定义域关于原点对称

2.基本类型：
$$\begin{array}{rl}1.& f(x)+f(-x)为偶函数，如\frac{e^x+e^{-x}}{2};\sqrt[3]{(1+x{)}^2}+\sqrt[3]{(1-x{)}^2}\\ 2.& f(x)-f(-x)为奇函数，如\frac{e^x-e^{-x}}{2}；\ln \frac{1+x}{1-x}\\ 3.& f[\psi (x)]为复合函数\\ & 奇[偶]=偶：sin{x}^2\\ & 偶[奇]=偶：cos(sinx);\mid sinx\mid \\ & 奇[奇]=奇：sin\frac{1}{x};\sqrt[3]{tanx}\\ & 偶[偶]=偶：cos\mid x\mid ;\mid cosx\mid \\ & 非[偶]=偶：e^{x^2};\ln \mid x\mid \\ 4.& 一个特殊函数：\ln (x+\sqrt{1+x^2})为奇函数\\ 5.& 求导后奇偶性互换\\ 6.& 以0为下限，求积分后奇偶性互换，如f(x)为奇函数，则{\int }_0^{x}f(t)dt为偶函数\\ 7.& (题源)f(x)连续,\forall x,y,使f(x+y)=f(x)+f(y)\to f(x)为奇函数\\ & 证明：取y=0,f(x)=f(x)+f(0)=f(0)=0；取y=-x,f(0)=f(x)+f(-x)\to f(x)=-f(-x)\end{array}$$

$$\begin{array}{rl}[例]& {\int }_{-1}^1\ln (x+\sqrt{1+x^2})e^{-x^2}dx=0,前者是4的奇函数，后者为偶函数，得奇函数\\ & {\int }_{-1}^1({\int }_0^x{e}^{-t^2}dt)x^{2}dx=0,前者为奇函数，后者为偶函数，得奇函数\\ & 以7为前置条件，{\int }_{-1}^1(x^2+1)f(x)dx=0,前者为偶函数，后者为奇函数，得奇函数\end{array}$$

3.变体类型（平移）：
$$\begin{array}{rl}& 1.f(x)为偶函数\to 关于y轴对称，即f(0+x)=f(0-x)(平移)得f(x)关于x=T对称，即f(T+x)=f(T-x)\\ & [例]f(x)为正值且连续，{\int }_{-\infty }^{+\infty }f(x)dx=1,又f(1+x)=f(1-x),且{\int }_0^{2}f(x)dx=0.6,则{\int }_{-\infty }^{0}f(x)dx=0.2\\ & 2.f(x)为奇函数\to 关于(0,0)对称，(平移)\to 关于(x_0,0)对称，如x^3\to (x-1{)}^3\\ & [例]{\int }_{-1}^1{x}^{3}dx=0;{\int }_0^2(x-1{)}^{3}dx=0;{\int }_0^4(x-2)dx=0\end{array}$$

4.奇偶性

$$\begin{array}{rl}& 偶函数\cdot 偶函数=偶函数奇函数\cdot 奇函数=偶函数奇函数\cdot 偶函数=奇函数\end{array}$$

5.总结

$$\begin{array}{rl}& {\int }_0^{x}f(t)dt⟸f(x)⟹f^{\prime }(x)奇偶性互换\\ & [注]f(x)奇\to {\int }_a^{x}f(t)dt={\int }_a^{0}f(t)dt+{\int }_0^{x}f(t)dt\\ [周期]& 1.f(x)T⟹{\int }_0^{T}f(x)dx={\int }_a^{a+T}f(x)dx,\forall a\\ & 2.若{\int }_0^{T}f(x)dx=0,则{\int }_a^{x}f(t)dt,f(x),f^{\prime }(x)周期都为T\\ & 3.f(x)T⟹{\int }_0^{nT}f(x)dx=n{\int }_0^{T}f(x)dx\end{array}$$

5.例题

$$\begin{array}{rl}[例1]& 设f(x)连续，F(x)={\int }_0^{x}f(t)dt证明:(1)F(x)的奇偶性与f(x)的奇偶性互换\\ & (2)若f(x)为奇函数，则一切原函数均为偶函数，若f(x)为偶函数，则只有一个原函数为奇函数\\ (1)& F(-x)={\int }_0^{-x}f(t)dt,令t=-u,则I={\int }_0^{x}f(-u)d(-u)\\ & \{\begin{array}{l}若f(x)奇函数⟹f(-u)=-f(u)⟹F(-x)={\int }_0^{x}f(u)du=F(x)\\ 若f(x)偶函数⟹f(-u)=f(u)⟹F(-x)=-{\int }_0^{x}f(u)du=-F(x)\end{array}\\ (2)& f(x)为奇函数⟹F(x)={\int }_0^{x}f(t)dt为偶函数\\ & {\int }_a^{x}f(t)dt={\int }_a^{0}f(t)dt+{\int }_0^{x}f(t)dt\\ & f(x)为偶函数⟹F(x)={\int }_0^{x}f(t)dt为奇函数，则为非奇函数\\ [例2]& 设f(x)连续，T为周期，证明(1){\int }_a^{a+T}f(x)dx={\int }_0^{T}f(x)dx,\forall a\\ & (2){\int }_0^{x}f(t)dt以T为周期⟺{\int }_o^{T}f(x)dx=0(3)\int f(x)dx以T为周期⟺{\int }_0^{T}f(x)dx=0\\ (1)& {\int }_a^{a+T}={\int }_a^{0}f(x)dx+{\int }_o^{T}f(x)dx+{\int }_T^{a+T}f(x)dx\\ & 其中令x-T=t,{\int }_T^{a+T}f(x)dx={\int }_0^{a}f(t+T)dt={\int }_0^{a}f(t)dt⟹{\int }_a^0+{\int }_0^a=0\\ & 故{\int }_a^{a+T}f(x)dx={\int }_0^{T}f(x)dx,\forall a\\ [注]& 若f(x)以T为周期，则其在一个周期上的积分值与起点无关\\ (2)& F(x)={\int }_0^{x}f(t)dt,F(x+T)-F(x)={\int }_0^{x+T}-{\int }_0^x={\int }_x^{x+T}f(t)dt\\ & 故F(x)以T为周期⟺{\int }_0^{T}f(t)dt=0\\ & 故(2)(3)⟹若f(x)以T为周期且{\int }_0^{T}f(x)dx=0\\ & \{\begin{array}{l}{\int }_0^{x}f(t)dt以T为周期\\ {\int }_a^{x}f(t)dt以T为周期\end{array}\\ [例3]& 若f(x)连续，则以下函数\\ & {\int }_0^{x}t[f(t)+f(-t)]dt为偶函数\\ & {\int }_0^{x}t[f(t)-f(-t)]dt为奇函数\\ & {\int }_0^{x}f(t^2)dt为奇函数\\ & {\int }_0^x{f}^2(t)dt为非负函数\\ [例4]& 设f(x)以T为周期，可导，则{\int }_a^{x}f(t)f^{\prime }(t)dt是否以T为周期？\\ & {\int }_0^{T}f(t)f^{\prime }(t)dt={\int }_0^{T}f(t)\frac{df(t)}{dt}dt=\frac{1}{2}{f}^2(t){|}_0^T=\frac{1}{2}[f^2(T)-f^2(0)]=0\end{array}$$

积分比大小

$$\begin{array}{rl}& 方法：\{\begin{array}{l}1.看出正负\\ 2.偶倍奇零\\ 3.作差换元\end{array}\\ [例1]& 设M={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{\sin x}{1+x^2}{\cos }^{6}xdx,N={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}({\sin }^{3}x+{\cos }^{6}x)dx,P={\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}(x^2{\sin }^{3}x-{\cos }^{6}x)dx,\\ & 试比较M,N,P的大小\\ & M=0,N=2{\int }_0^{\frac{\pi }{2}}{\cos }^{6}xdx>0,P=-2{\int }_0^{\frac{\pi }{2}}{\cos }^{6}xdx<0\\ & 故N>M>P\\ [例2]& 设F(x)={\int }_x^{x+2\pi }{e}^{\sin t}\sin tdt,则F(x)=\underline{}\\ & F^{\prime }(x)=e^{\sin (x+2\pi )}\sin (x+2\pi )-e^{\sin x}\sin x=0\\ & ⟹F(x)=c=F(0)={\int }_0^{2\pi }{e}^{\sin t}\sin tdt>0\\ & 故F(x)为正常数\\ [例3]& 设I_k={\int }_0^{k\pi }{e}^{x^2}\sin xdx(k=1,2,3),则有:()\\ & A.I_1<I_2<I_{3}B.I_3<I_2<I_{1}C.I_2<I_3<I_{1}D.I_2<I_1<I_3\\ & I_1={\int }_0^{\pi }{e}^{x^2}\sin xdx,I_2={\int }_0^{2\pi }{e}^{x^2}\sin xdx,I_3={\int }_0^{3\pi }{e}^{x^2}\sin xdx\\ & 画图知该函数随着横坐标x的增大，其因式e^{x^2}也会增大，故其凹或凸的区间会增大\\ & I_1>0,I_2<0,I_3>I_1>0\\ [例4]& 设常数a>0,积分I_1={\int }_0^{\frac{\pi }{2}}\frac{\cos x}{1+x^{\alpha }}dx,I_2={\int }_0^{\frac{\pi }{2}}\frac{\sin x}{1+x^{\alpha }}dx,则()\\ & I_1-I_2={\int }_0^{\frac{\pi }{2}}\frac{1}{1+x^{\alpha }}(\cos x-\sin x)dx\\ & ={\int }_0^{\frac{\pi }{4}}\frac{1}{1+x^{\alpha }}(\cos x-\sin x)dx+{\int }_{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{1}{1+x^{\alpha }}(\cos x-\sin x)dx>0(前者大，后者小)\\ & A.I_1>I_{2}B.I_1<I_{2}C.I_1=I_{2}D.大小与\alpha 有关\\ [例5]& 证明{\int }_0^1\frac{x\cdot \sin \frac{\pi }{2}x}{1+x}dx>{\int }_0^1\frac{x\cdot \cos \frac{\pi }{2}x}{1+x}dx\\ & I_{左}-I_{右}={\int }_0^1\frac{x}{1+x}(\sin \frac{\pi }{2}x-\cos \frac{\pi }{2}x)dx\\ & ={\int }_0^{\frac{1}{2}}\frac{x}{1+x}(\sin \frac{\pi }{2}x-\cos \frac{\pi }{2}x)dx+{\int }_{\frac{1}{2}}^1\frac{x}{1+x}(\sin \frac{\pi }{2}x-\cos \frac{\pi }{2}x)dx>0\end{array}$$

定积分定义

很早人们就发现了一个矩形的面积是底*高，而一个边为曲线的图形呢？

黎曼（1826-1866）发现，将这种图形任意分割成n份，就可以粗略的看到一个个小矩形。

随着分割地越来越多，矩形也就变的越来越细。

一个矩形的面积是可以求得的，那么当这些矩形无限细的时候就可以通过求他们的面积和来得到曲边图形的面积，由于是黎曼最早提出的，定积分也叫做黎曼积分。

$$\begin{array}{rl}& 1.[a,b]n等分，每段长度为\frac{b-a}{n}\\ & 2.取右端点的高\to f(a+\frac{b-a}{n}i)\\ & \therefore \underset{n\to \infty }{\lim }\sum _{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}={\int }_a^{b}f(x)dx\\ [小结]& 1.\underset{x\to \infty }{\lim }\sum _{i=1}^n=\underset{x\to \infty }{\lim }\sum _{i=0}^{n-1}（区别是前者取右端点，后者取左端点）\\ & 2.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(a+\frac{b-a}{n}i)\frac{b-a}{n}={\int }_a^{b}f(x)dx\\ & 3.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(0+\frac{1-0}{n}i)\frac{1-0}{n}={\int }_0^{1}f(x)dx\\ & 4.\underset{x\to \infty }{\lim }\sum _{i=1}^{n}f(0+\frac{x-0}{n}i)\frac{x-0}{n}={\int }_0^{x}f(t)dt\\ & 详细题目上一致数列极限部分\end{array}$$

反常积分判敛

$$\begin{array}{rl}& {\int }_1^{+\infty }\frac{1}{X^P}dx\{\begin{array}{l}收敛，P>1\\ 发散，P\le 1\end{array}\\ & {\int }_0^1\frac{1}{X^P}dx\{\begin{array}{l}收敛，0<P<1\\ 发散，P>1\end{array}\\ [注]& 判敛时，每个积分中含且仅含一个奇点\\ [例1]& a,b>0,{\int }_0^{+\infty }\frac{1}{x^a(2020+x{)}^b}dx收敛，则\underline{}\\ & 拆{\int }_0^1\frac{1}{x^a(2020+x{)}^b}dx+{\int }_1^{+\infty }\frac{1}{x^a(2020+x{)}^b}dx\\ & 1.x\to 0^{+}⟹a<1\\ & 2.x\to +\infty ⟹2020+x\to +\infty ⟹{\int }_1^{+\infty }\frac{1}{x^{a+b}}dx⟹a+b>1\\ [例2]& a>b>0,{\int }_0^{+\infty }\frac{1}{x^a+x^b}dx收敛,则\underline{}\\ & {\int }_0^{+\infty }\frac{1}{x^a+x^b}dx={\int }_0^1\frac{1}{x^a+x^b}dx+{\int }_1^{+\infty }\frac{1}{x^a+x^b}dx\\ & 1.x\to 0^{+},x^a+x^b\sim x^b⟹{\int }_0^1\frac{1}{x^b}dx⟹b<1\\ & 2.x\to +\infty ,x^a+x^b\sim x^a⟹{\int }_1^{+\infty }\frac{1}{x^a}dx⟹a>1\end{array}$$

计算与应用

基本积分表

$$\begin{array}{rl}& \int x^{k}dx=\frac{1}{k+1}{x}^{k+1}+C,k̸=-1\int \frac{1}{x^2}dx=-\frac{1}{x}+C\int \frac{1}{\sqrt{x}}dx=2\sqrt{x}+C\\ & \int \frac{1}{x}dx=\ln |x|+C\int e^{x}dx=e^x+C\int a^{x}dx=\frac{1}{\ln a}{a}^x+C(a>0\&a̸=1)\\ & \int \sin xdx=-\cos x+C\int \cos xdx=\sin x+C\int \tan xdx=-\ln |\cos x|+C\\ & \int \cot xdx=\ln |\sin x|+C\int \frac{dx}{\cos x}=\int \sec xdx=\ln |\sec x+\tan x|+C\\ & \int \frac{dx}{\sin x}=\int \csc xdx=\ln |\csc x-\cot x|+C\int {\sec }^{2}xdx=\tan x+C\\ & \int {\csc }^{2}xdx=-\cot x+C\int \sec x\tan xdx=\sec x+C\int {\csc }^{2}xdx=-\cot x+C\\ & \int \frac{1}{1+x^2}dx=\arctan x+C\int \frac{1}{a^2+x^2}dx=\frac{1}{a}\arctan \frac{x}{a}+C\\ & \int \frac{1}{1-x^2}dx=\arcsin x+C\int \frac{1}{\sqrt{a^2-x^2}}dx=\arcsin \frac{x}{a}+C\\ & \int \frac{1}{\sqrt{x^2+a^2}}dx=\ln (x+\sqrt{x^2+a^2})+C\int \frac{1}{\sqrt{x^2-a^2}}dx=\ln (x+\sqrt{x^2-a^2})+C\\ & \int \frac{1}{x^2-a^2}dx=\frac{1}{2a}\ln |\frac{x-a}{x+a}|+C\int \frac{1}{a^2-x^2}dx=\frac{1}{2a}\ln |\frac{x+a}{x-a}|+C\\ & \int \sqrt{a^2-x^2}dx=\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C\end{array}$$

不定积分计算

凑微分法

$$\begin{array}{rl}& 于两边加d(取微分)，即d(\int x^{k}dx)=d(\frac{1}{k+1}{x}^{k+1}+C)\\ 1.& dx=\frac{1}{a}d(ax+b),a̸=0\\ 2.& x^{k}dx=\frac{1}{k+1}d(x^{k+1}),k̸=1且̸=0xdx=\frac{1}{2}d{x}^2\frac{1}{x^2}dx=d(-\frac{1}{x})\frac{1}{\sqrt{x}}dx=2d\sqrt{x}\sqrt{x}dx=\frac{2}{3}d{x}^{\frac{3}{2}}\\ 3.& \frac{1}{x}dx=d\ln x,x>0\\ 4.& e^{x}dx=d{e}^x{a}^{x}dx=\frac{1}{\ln a}d{a}^x\\ 5.& \sin xdx=d(-\cos x)\cos xdx=d(\sin x)\\ 6.& \frac{1}{{\cos }^{2}x}dx={\sec }^{2}xdx=d(\tan x)\frac{dx}{{\sin }^{2}x}={\csc }^{2}xdx=d(-\cot x)\\ 7.& \frac{1}{1+x^2}dx=d(\arctan x)\\ 8.& \frac{1}{\sqrt{1-x^2}}dx=d(\arcsin x)\end{array}$$

$$\begin{array}{rl}& [例1]\int (1+x-\frac{1}{x})e^{x+\frac{1}{x}}dx=\int e^{x+\frac{1}{x}}dx+\int x(1-\frac{1}{x^2})e^{x+\frac{1}{x}}dx=\int e^{x+\frac{1}{x}}dx+\int x\cdot e^{x+\frac{1}{x}}d(x+\frac{1}{x})\\ & =\int e^{x+\frac{1}{x}}dx+\int x\cdot d{e}^{x+\frac{1}{x}}=x\cdot e^{x+\frac{1}{x}}+C\end{array}$$

分部积分法

$$\begin{array}{rl}[使用场合]& 不同函数类型乘积\\ [公式]& \int udv=uv-\int vdu\\ [原则]& 谁易求导谁做u,谁易积分谁做v,u\underleftrightarrow{反对幂指三}v\\ [证明]& (uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }⟹\int (uv{)}^{\prime }=\int u^{\prime }v+\int u{v}^{\prime }⟹\\ & \int \frac{d(uv)}{dx}=\int \frac{du}{dx}v+\int \frac{dv}{dx}u⟹\int d(uv)=\int vdu+\int u\cdot dv\\ [表格法]& 多次分部积分时，可用表格法\\ & x^2\to 2x\to 2\to 0e^x\to e^x\to e^x\to e^x\\ & \int x^2{e}^{x}dx=\int x^{2}d{e}^x=x^2{e}^x-\int e^x\cdot 2xdx=x^2{e}^x-2\int xd{e}^x\\ & =x^2{e}^x-2x{e}^x+2\int e^{x}dx=x^2+e^x-2x{e}^x+2e^x+C\\ & \begin{array}{cccc}{x}^2& 2x& 2& 0\\ e^x& +e^x& -e^x& +e^x\end{array}\\ & \int x^2{e}^{x}dx=x^2{e}^x-2x{e}^x+2e^x+C\\ [证明]& \int u{v}^{\prime \prime \prime }dx=\int ud{v}^{\prime \prime }=u{v}^{\prime \prime }-\int v^{\prime \prime }{u}^{\prime }dx\\ & \int u^{\prime }{v}^{\prime \prime }dx=\int u^{\prime }d{v}^{\prime }=u^{\prime }{v}^{\prime }-\int v^{\prime }{u}^{\prime \prime }dx\\ & \int u^{\prime \prime }{v}^{\prime }dx=\int u^{\prime \prime }dv=u^{\prime \prime }v-\int v{u}^{\prime \prime \prime }dx\\ & ⟹\int u{v}^{\prime \prime \prime }dx=u{v}^{\prime \prime }-u^{\prime }{v}^{\prime }+u^{\prime \prime }v-\int v{u}^{\prime \prime \prime }dx\\ & \begin{array}{cccc}u& u^{\prime }& u^{\prime \prime }& u^{\prime \prime \prime }\\ v^{\prime \prime \prime }& +v^{\prime \prime }& -v^{\prime }& +v\end{array}\end{array}$$

$$\begin{array}{rl}[例1]& \int \frac{x\ln (x+\sqrt{1+x^2})}{(1+x^2{)}^2}dx\\ & =\frac{1}{2}\int \ln (x+\sqrt{1+x^2})\frac{d(x^2+1)}{(x^2+1{)}^2}\\ & =\frac{1}{2}\int \ln (x+1\sqrt{1+x^2})d(-\frac{1}{x^2+1})\\ & =-\frac{1}{2}[\frac{ln(x+\sqrt{1+x^2})}{x^2+1}-\int \frac{1}{x^2+1}\cdot \frac{1}{\sqrt{1+x^2}}dx]\\ & =-\frac{1}{2}\cdot \frac{\ln (x+\sqrt{1+x^2})}{x^2+1}+\frac{1}{2}\int \frac{1}{(1+x^2{)}^{\frac{3}{2}}}dx\\ [例2]& {\int }_0^{+\infty }\frac{x{e}^{-3x}}{(1+e^{-3x}{)}^2}dx\\ & ={\int }_0^{+\infty }\frac{x{e}^{3x}}{(1+e^{3x}{)}^2}dx\\ & =\frac{1}{3}{\int }_0^{+\infty }x\cdot \frac{d(e^{3x}+1)}{(1+e^{3x}{)}^2}\\ & =-\frac{1}{3}{\int }_0^{+\infty }xd\frac{1}{1+e^{3x}}\\ & =-\frac{1}{3}\frac{x}{1+e^{3x}}+\frac{1}{3}{\int }_0^{+\infty }\frac{1}{1+e^{3x}}dx\\ & =-\frac{1}{3}\frac{x}{1+e^{3x}}+\frac{1}{3}{\int }_0^{+\infty }\frac{e^{3x}}{e^{3x}(1+e^{3x})}dx\\ & =-\frac{1}{3}\frac{x}{1+e^{3x}}+\frac{1}{9}{\int }_0^{+\infty }\frac{d{e}^{3x}}{e^{3x}(1+e^{3x})}\\ & =-\frac{1}{3}\frac{x}{1+e^{3x}}{|}_0^{+\infty }+\frac{1}{9}\ln \frac{e^{3x}}{1+e^{3x}}{|}_0^{+\infty }\\ & =(0-0)+\frac{1}{9}(0-\ln \frac{1}{2})=\frac{1}{9}\ln 2\\ [例3]& 设\frac{\ln x}{x}是f(x)的一个原函数，则{\int }_1^{e}x{f}^{\prime }(x)dx=\\ & (\frac{\ln x}{x}{)}^{\prime }=f(x)=\frac{1-\ln x}{x^2}\\ & 已知f(x)的表达式\int x{f}^{\prime }(x)dx=\int xdf(x)=xf(x)-\int f(x)dx(降阶题)\\ & \therefore f(x)=(\frac{\ln x}{x}{)}^{\prime }=\frac{1-\ln x}{x^2}⟹{\int }_1^{e}x{f}^{\prime }(x)dx={\int }_1^{e}xdf(x)\\ & =xf(x){|}_1^e-{\int }_1^{e}f(x)dx=\frac{1-\ln x}{x}{|}_1^e-\frac{\ln x}{x}{|}_1^e\\ & =(0-1)-(\frac{1}{e}-0)=-1-\frac{1}{e}\\ [例4]& 设f(x)={\int }_0^x{e}^{-t^2+2t}dt,求{\int }_0^1(x-1{)}^{2}f(x)dx\\ & f^{\prime }(x)=e^{-x^2+2x}\\ & \int (x-1{)}^{2}f(x)dx=\frac{1}{3}\int f(x)d(x-1{)}^3=\frac{1}{3}[(x-1{)}^{3}f(x)-\int (x-1{)}^3{f}^{\prime }(x)dx](升阶题)\\ & I=\frac{1}{3}{\int }_0^{1}f(x)d(x-1{)}^3=\frac{1}{3}f(x)\cdot (x-1{)}^3{|}_0^1-\frac{1}{3}{\int }_0^1(x-1{)}^3{f}^{\prime }(x)dx\\ & =\frac{1}{3}(0-0)-\frac{1}{3}{\int }_0^1(x-1{)}^3{e}^{-x^2+2x}dx\\ & =-\frac{1}{3}{\int }_0^1(x-1{)}^2{e}^{-(x-1{)}^2}ed(x-1{)}^2\\ & 令(x-1{)}^2=t,I=-\frac{e}{6}{\int }_1^{0}t{e}^{-t}dt\\ & =\frac{e}{6}{\int }_0^{1}t{e}^{-t}dt=\frac{e}{6}(-t{e}^{-t}-e^{-t}){|}_0^1=\frac{1}{6}(e-2)\\ [总结]& \{\begin{array}{l}1.反对幂指三\\ 2.表格法\\ 3.升阶、降阶题\end{array}\end{array}$$

换元法

$$\begin{array}{rl}& 1.\sqrt{a^2-x^2}⟹x=a\sin t2.\sqrt{a^2+x^2}⟹x=a\tan t3.\sqrt{x^2-a^2}⟹x=a\sec t\\ & 4.\sqrt{a{x}^2+bx+c}⟹\{\begin{array}{l}\sqrt{k^2-{\psi }^2(x)}\\ \sqrt{k^2+{\psi }^2(x)}\\ \sqrt{{\psi }^2(x)-k^2}\end{array}\\ & 5.\begin{array}{l}\sqrt[n]{ax+b}=t\\ \sqrt{\frac{ax+b}{cx+d}}=t\\ \sqrt{a{e}^{bx}+e}=t\end{array}\}\sqrt{\ast }=t(根式代换)\sqrt[n_1]{ax+b},\sqrt[n_2]{ax+b},令\sqrt[n]{ax+b}=t,n为以上的公倍数\\ & 6.倒代换\frac{1}{x^n},n\ge 2⟹\frac{1}{x}=t7.a^x,e^x,\arcsin x,\arctan x,\ln x=t\\ [注]& \int P_n(x)\cdot a^{x}dx,优先分部积分法\end{array}$$

$$\begin{array}{rl}[例1]& {\int }_0^1\arcsin \sqrt[3]{x}dx\\ & 令\arcsin \sqrt[3]{x}=t⟹\sin (\arcsin \sqrt[3]{x})=\sin t\\ & ⟹x={\sin }^{3}t⟹I={\int }_0^{\frac{\pi }{2}}td{\sin }^{3}t=t{\sin }^{3}t{|}_0^{\frac{\pi }{2}}-{\int }_0^{\frac{\pi }{2}}{\sin }^{3}tdt\\ & =\frac{\pi }{2}-{\int }_0^{\frac{\pi }{2}}{\sin }^{3}tdt=\frac{\pi }{2}-\frac{2}{3}\\ [注]& 华里士公式，点火公式\\ & {\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx={\int }_0^{\frac{\pi }{2}}{\cos }^{n}xdx=\{\begin{array}{l}\frac{n-1}{n}\cdot \frac{n-3}{n-2}\cdots \frac{1}{2}\frac{\pi }{2},n为正偶数\\ \frac{n-1}{n}\cdots \frac{2}{3},n为大于1的奇数\end{array}\\ [例2]& 求y=x\cdot \sqrt{4x-x^2}在[0,4]上的图形绕y轴的体积\\ & V_y={\int }_0^{4}2\pi x^2\sqrt{4x-x^2}dx=2\pi {\int }_0^4{x}^2\sqrt{(4-x)x}dx\\ & 令x=4{\sin }^{2}t,I=2\pi {\int }_0^{\frac{\pi }{2}}16{\sin }^{4}t\cdot 4\sin t\cdot \cos t\cdot 4(2\sin t\cos t)dt\\ & =2^{10}\pi {\int }_0^{\frac{\pi }{2}}{\sin }^{6}t(1-{\sin }^{2}t)dt=2^{10}\pi [(\frac{5}{6}\cdot \frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi }{2})-(\frac{7}{8}\cdot \frac{5}{6}\cdot \frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi }{2})]=20{\pi }^2\\ [注]& 区间再现公式\\ & 令x=a+b-t,则{\int }_a^{b}f(x)dx={\int }_b^{a}f(a+b-t)(-dt)={\int }_a^{b}f(a+b-t)dt\\ & 故{\int }_a^{b}f(x)dx={\int }_a^{b}f(a+b-x)dx\\ [例3]& {\int }_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{2^{x-1}}{2^x+1}{\cos }^{4}2xdx\\ & I=\frac{1}{2}{\int }_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{2^x}{2^x+1}{\cos }^{4}2xdx,令x=-t，得:\\ & \frac{1}{2}{\int }_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{1}{2^t+1}{\cos }^{4}2tdt⟹2I=\frac{1}{2}{\int }_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{2^x+1}{2^x+1}{\cos }^{4}2xdx,令2x=u，得\\ & \frac{1}{2}{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{4}}{\cos }^{4}u\frac{du}{2}=\frac{1}{2}{\int }_0^{\frac{\pi }{2}}{\cos }^{4}udu\\ & I=\frac{1}{4}{\int }_0^{\frac{\pi }{2}}{\cos }^{4}udu=\frac{1}{4}\frac{3}{4}\frac{1}{2}\frac{\pi }{2}=\frac{3}{64}\pi \\ [例4]& {\int }_0^2[(x-1{)}^3+2x]\sqrt{1-\cos 2\pi x}dx\\ & 令x-1=t,得{\int }_{-1}^1(t^3+2t+2)\sqrt{1-\cos 2\pi t}dt=4{\int }_0^1\sqrt{1-\cos 2\pi t}dt\\ & =4\sqrt{2}{\int }_0^1\sin \pi tdt=4\sqrt{2}(-\frac{1}{\pi }\cos \pi t){|}_0^1=4\sqrt{2}(\frac{1}{\pi }+\frac{1}{\pi })=\frac{8\sqrt{2}}{\pi }\end{array}$$

有理函数积分

$$\begin{array}{rl}1.& 有理函数：\int \frac{P_n(x)}{Q_m(x)}dx(n<m)\\ 2.& 对Q_m(x)进行因式分解\\ & \frac{P_n(x)}{(ax+b{)}^k}=\frac{A_1}{ax+b}+\frac{A_2}{(ax+b{)}^2}+\cdots +\frac{A_k}{(ax+b{)}^k}\\ & \frac{P_n(x)}{(p{x}^2+qx+r{)}^k}=\frac{A_{1}x+B_1}{p{x}^2+qx+r}+\frac{A_{2}x+B_2}{(p{x}^2+qx+r{)}^2}+\cdots +\frac{A_{k}x+B_k}{(p{x}^2+qx+r{)}^k}\end{array}$$

$$\begin{array}{rl}[例1]& 求\int \frac{4x^2-6x-1}{(x+1)(2x-1{)}^2}dx\\ & \frac{4x^2-6x-1}{(x+1)(2x-1{)}^2}=\frac{A}{x+1}+\frac{B}{(2x-1{)}^1}+\frac{C}{(2x-1{)}^2}\\ & ⟹4x^2-6x-1\equiv A(2x-1{)}^2+B(2x-1)(x+1)+C(x+1)\\ & 令x=-1⟹4+6-1=9A⟹A=1\\ & 令x=\frac{1}{2}⟹1-3-1=C\cdot \frac{3}{2}⟹C=-2\\ & 令x=0⟹-1=1-B-2⟹B=0\\ & I=\int \frac{1}{x+1}dx-2\int \frac{1}{(2x-1{)}^2}dx=\ln |x+1|+\frac{1}{2x-1}+C\\ [例2]& {\int }_1^{+\infty }\frac{dx}{x^2(x+1)}\\ & \frac{1}{x^2(x+1)}=\frac{A}{x+1}+\frac{Bx+C}{x^2}⟹1\equiv A{x}^2+(Bx+C)(x+1)\\ & \{\begin{array}{l}令x=01=c\\ 令x=-11=A\\ x^2前系数0=A+B⟹B=-1\end{array}\\ & ⟹{\int }_1^{+\infty }\frac{1}{x^2(x+1)}dx={\int }_1^{+\infty }(\frac{1}{x+1}+\frac{1-x}{x^2})dx={\int }_1^{+\infty }(\frac{1}{x+1}+\frac{1}{x^2}-\frac{1}{x})dx\\ & ={\int }_1^{+\infty }(\frac{1}{x+1}-\frac{1}{x})dx+{\int }_1^{+\infty }\frac{1}{x^2}dx=\ln \frac{x+1}{x}{|}_1^{+\infty }+(-\frac{1}{x}{|}_1^{+\infty })=1-\ln 2\end{array}$$

变现积分计算

直接求导型

$$\begin{array}{rl}[例1]& f(x)连续且>0,则方程{\int }_a^{x}f(t)dt+{\int }_b^x\frac{1}{f(t)}dt=0,在(a,b)内有\underline{}个根\\ & 令F(x)={\int }_a^{x}f(t)dt+{\int }_b^x\frac{1}{f(t)}dt\\ & 则F^{\prime }(x)=f(x)+\frac{1}{f(x)}>0⟹F(x)单调递增\\ & F(a)={\int }_b^a\frac{1}{f(t)}dt=-{\int }_a^b\frac{1}{f(t)}dt<0,F(b)={\int }_a^{b}f(t)dt>0\\ & 即有一个根\\ [例2]& 设f(x)为连续函数，且F(x)={\int }_{\frac{1}{x}}^{\ln x}f(t)dt,则F(x)=\\ & F^{\prime }(x)=f(\ln x)\cdot \frac{1}{x}-f(\frac{1}{x})(\frac{-1}{x^2})\\ [例3]& \underset{x\to 0}{\lim }{\int }_0^x\frac{\sin 2t}{\sqrt{4+t^2}{\int }_0^x(\sqrt{t+1}-1)dt}dt\\ & I=\underset{x\to 0}{\lim }\frac{{\int }_0^x\frac{\sin 2t}{\sqrt{4+t^2}}dt}{{\int }_0^x(\sqrt{t+1}-1)dt}=\underset{x\to 0}{\lim }\frac{\frac{\sin 2x}{\sqrt{4+x^2}}}{\sqrt{x+1}-1}\\ & =\frac{1}{2}\underset{x\to 0}{\lim }\frac{\sin 2x}{\sqrt{1+x}-1}=2\\ [例4]& \underset{x\to 0}{\lim }\frac{{\int }_0^x[{\int }_0^{u^2}\arctan (1+t)dt]du}{x(1-\cos x)}\\ & 令\phi (u)={\int }_0^{u^2}\arctan (1+t)dt\\ & 则I=\underset{x\to 0}{\lim }\frac{{\int }_0^x\phi (u)du}{x\cdot \frac{1}{2}{x}^2}=\underset{x\to 0}{\lim }\frac{\phi (x)}{\frac{3}{2}{x}^2}\\ & \underset{x\to 0}{\lim }\frac{{\int }_0^{x^2}\arctan (1+t)dt}{\frac{3}{2}{x}^2}\\ & \underset{x\to 0}{\lim }\frac{\arctan (1+x^2)\cdot 2x}{3x}=\frac{\pi }{6}\end{array}$$

拆分求导型

$$\begin{array}{rl}& 设\phi (x)在[a,b]上连续，且\phi (x)>0,则函数y={\int }_a^b|x-t|\phi (t)dt,则()\\ & A.在(a,b)内为凸B.在(a,b)内为凹C.在(a,b)内有拐点D.在(a,b)内有间断点\\ y& ={\int }_a^b|x-t|\phi (t)dt\\ & ={\int }_a^x(x-t)\phi (t)dt+{\int }_x^b(t-x)\phi (t)dt\\ & ={\int }_a^{x}x\phi (t)dt-{\int }_a^{x}t\cdot \phi (t)dt+{\int }_x^{b}t\phi (t)dt-{\int }_x^{b}x\phi (t)dt\\ & =x{\int }_a^x\phi (t)dt-{\int }_a^{x}t\phi (t)dt+{\int }_x^{b}t\phi (t)dt-x{\int }_x^b\phi (t)dt\\ & ⟹y^{\prime }={\int }_a^x\phi (t)dt+x\phi (x)-x\phi (x)-x\phi (x)-{\int }_x^b\phi (t)dt+x\phi (x)\\ & ={\int }_a^x\phi (t)dt-{\int }_x^b\phi (t)dt⟹y^{\prime \prime }=\phi (x)+\phi (x)=2\phi (x)>0,故选B\end{array}$$

换元求导型

$$\begin{array}{rl}& 设f(x)在[0,+\infty )上可导，f(0)=0,其反函数为g(x),若{\int }_x^{x+f(x)}g(t-x)dt=x^2\ln (1+x),求f(x)\\ & {\int }_x^{x+f(x)}g(t-x)dt\underrightarrow{令u=t-x}{\int }_0^{f(x)}g(u)du\\ & ⟹{\int }_0^{f(x)}g(u)du=x^2\ln (1+x)⟹g(f(x))\cdot f^{\prime }(x)=2x\ln (1+x)+\frac{x^2}{1+x}\\ & ⟹x\cdot f^{\prime }(x)=2x\ln (1+x)+\frac{x^2}{1+x}\\ & ⟹f^{\prime }(x)=2\ln (1+x)+\frac{x}{1+x}\\ & ⟹f(x)=2\int \ln (1+x)dx+\int \frac{x}{1+x}dx\\ & =2(x+1)\ln (1+x)-2\int (x+1)\cdot \frac{1}{1+x}dx\\ & =2(x+1)\ln (1+x)-2x+x-\ln (1+x)+c\\ & 又f(0)=0,故c=0\\ & 则f(x)=(2x+1)\ln (1+x)-x\end{array}$$

应用

$$\begin{array}{rl}面积:& S={\int }_a^b{\circ }^{1}dx\\ 体积:& V_x={\int }_a^b\pi {\circ }^{2}dx\\ & V_y={\int }_a^{b}2\pi \cdot x{\circ }^{1}dy\end{array}$$