PCA主成分分析原理及其python代码复现-程序员宅基地
技术标签: python 机器学习 python数据分析 开发语言
PCA(主成分分析)是什么
降维算法:保留原始数据的关键信息
注意:在降维过程中,维度通常是指特征的数量,而不是空间的维度。
主成分分析(PCA)是一个常见的特征提取方法,它通过找到数据中的主成分(方差最大的方向)来实现降维。
通俗理解,就是寻找新的坐标系,使得数据尽可能分布在一个或几个坐标轴上,同时尽可能保留原先数据分布的主要信息,使原先高维度的信息,在转换后能用低维度的信息来保存。而新坐标系的坐标轴,称为主成分(Principal components, PC),这也就是PCA的名称来源。
为什么找方差最大的方向?
在信号处理领域中认为信号具有较大的方差,噪声有较小的方差;信噪比就是信号与噪声的方差比,越大意味着数据的质量越好。
PCA(主成分分析)用来干什么的,好处
通过保留主要特征来捕捉数据的重要结构,使得模型更快收敛。
展开来说,PCA去除噪声和不重要的特征,将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息,而且可以提升数据处理的速度。
PCA(主成分分析)怎么实现的(三步)
PCA方法的总结
标准化(去中心化);
从协方差矩阵或相关矩阵中获取特征向量和特征值,或执行奇异值分解SVD;
按降序对特征值进行排序,并选择 k k k个与最大特征值相对应的特征向量,其中 k k k是新特征子空间的维数( k ≤ p k≤p k≤p);
将选择的 k k k个特征向量构造为投影矩阵 W W W;
通过 W W W对原始数据集 X X X进行变换,得到 k k k维特征子空间 Y Y Y。
准备数据集
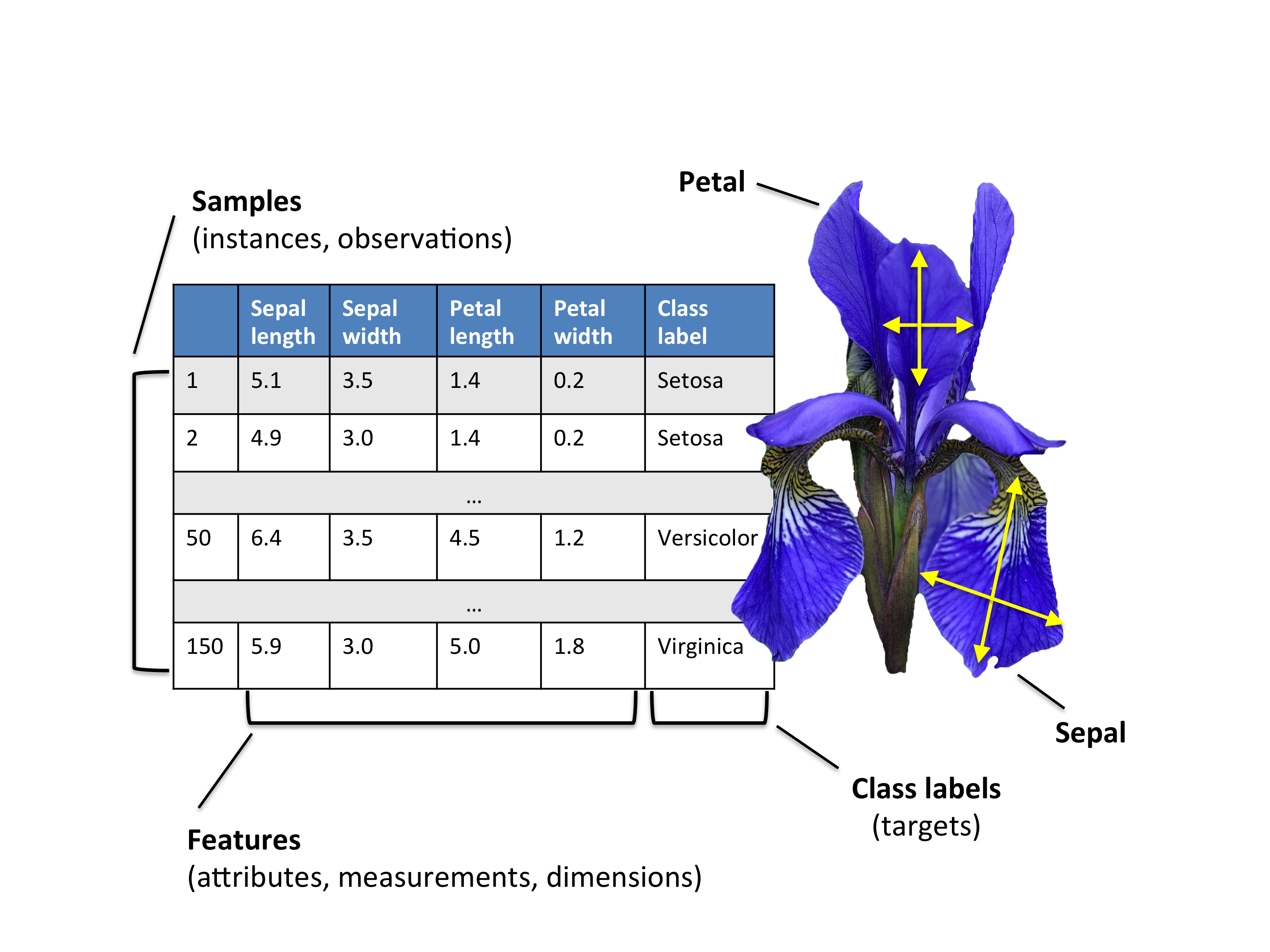
关于Iris数据集
scikit-learn中的鸢尾花数据集(Iris dataset),一共包含150张图片。
3种鸢尾花:山鸢尾(50张)、杂色鸢尾(50张)、维吉尼亚鸢尾(50张)。
4个特征:萼片长度(厘米)、萼片宽度(厘米)、花瓣长度(厘米)、花瓣宽度(厘米)。
加载数据集
加载数据集
import pandas as pd
# load-dataset
df = pd.read_csv(
filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
header=None,
sep=',')
df.columns = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.dropna(how="all", inplace=True) # drops the empty line at file-end
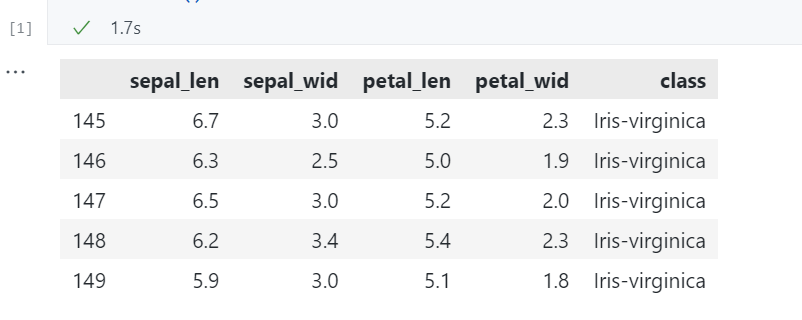
df.tail()
运行结果
划分成 数据 X X X、标签 y y y
# split data table into data X and class labels y
X = df.iloc[:, 0:4].values
y = df.iloc[:, 4].values
数据集为 150 × 4 150×4 150×4的矩阵,不同列代表不同特征,每行为1个样本,每个样本行x可以被描述为一个4维向量。
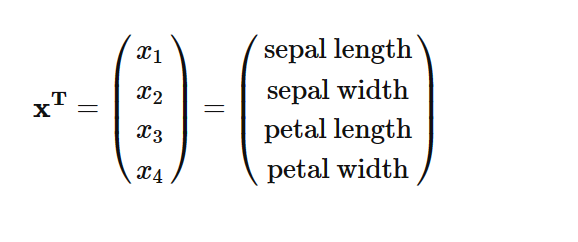
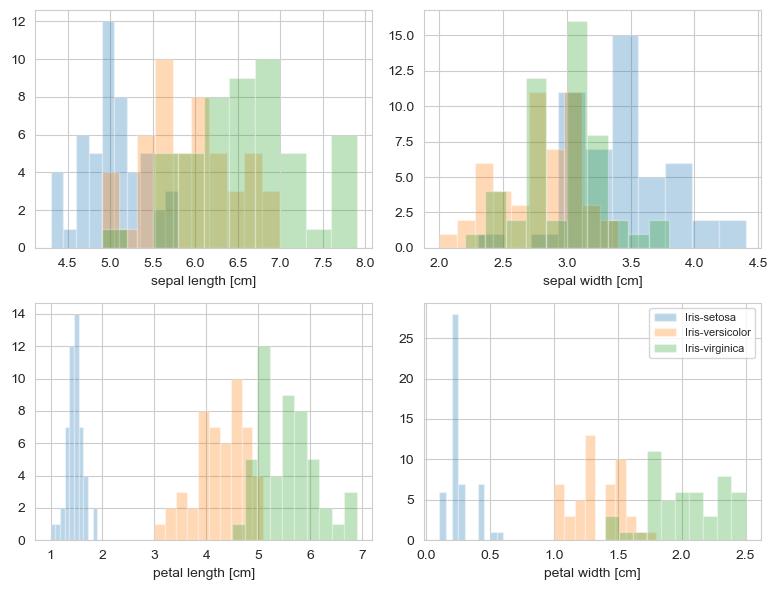
可视化数据分布
from matplotlib import pyplot as plt
import seaborn as sns
# 设置 seaborn 的样式为 whitegrid
sns.set_style("whitegrid")
label_dict = {
1: 'Iris-Setosa',
2: 'Iris-Versicolor',
3: 'Iris-Virgnica'}
feature_dict = {
0: 'sepal length [cm]',
1: 'sepal width [cm]',
2: 'petal length [cm]',
3: 'petal width [cm]'}
plt.figure(figsize=(8, 6))
for cnt in range(4):
plt.subplot(2, 2, cnt + 1)
for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
plt.hist(X[y == lab, cnt],
label=lab,
bins=10,
alpha=0.3, )
plt.xlabel(feature_dict[cnt])
plt.legend(loc='upper right', fancybox=True, fontsize=8)
plt.tight_layout()
plt.show()
运行结果
标准化
归一化:将数据映射到[0,1]或[-1,1]区间范围内,不同特征的量纲不同,值范围大小不同,存在奇异值,对训练有影响。
标准化:将数据映射到满足标准正态分布的范围内,使数据满足均值为0,标准差为1。
去中心化:使数据满足均值为0,但对标准差没有要求。
每种方法对应的使用场景
1.若对数据的范围没有限定要求,则选择标准化进行数据预处理
2.若要求数据在某个范围内取值,则采用归一化。
3若数据不存在极端的极大极小值时,采用归一化。
4.若数据存在较多的异常值和噪音,采用标准化。
标准化过程如下:
1、计算每个特征(每一列,共p个特征)的均值 x i ˉ \bar{x_i} xiˉj和标准差 S j S_j Sj,公式如下: x i ˉ = 1 n ∑ i = 1 n x i j \bar{x_i}=\frac{1}{n}\sum_{i=1}^nx_{ij} xiˉ=n1i=1∑nxij S j = ∑ i = 1 n ( x i j − x j ˉ ) 2 n − 1 S_j=\sqrt{\frac{\sum_{i=1}^n(x_{ij}-\bar{x_j})^2}{n-1}} Sj=n−1∑i=1n(xij−xjˉ)2
2、将每个样本的每个特征进行标准化处理,得到标准化特征矩阵 X s t a n d X_{stand} Xstand:
X i j = x i j − x j ˉ S j X_{ij}=\frac{x_{ij}-\bar{x_j}}{S_j} Xij=Sjxij−xjˉ
X s t a n d = [ X 11 X 12 ⋯ X 1 p X 21 X 22 ⋯ X 2 p ⋮ ⋮ ⋱ ⋮ X n 1 X n 2 ⋯ X n p ] = [ X 1 , X 2 , ⋯ , X p ] X_{stand} = \begin{bmatrix} X_{11} & X_{12} & \cdots & X_{1p} \\ X_{21} & X_{22} & \cdots & X_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ X_{n1} & X_{n2} & \cdots & X_{np} \\ \end{bmatrix} = \left[ \mathbf{X}_1, \mathbf{X}_2, \cdots, \mathbf{X}_p \right] Xstand= X11X21⋮Xn1X12X22⋮Xn2⋯⋯⋱⋯X1pX2p⋮Xnp =[X1,X2,⋯,Xp]
标准化是沿着每个特征(即每列)独立进行的。换句话说,对于 X 中的每一列(即每一个特征),StandardScaler 会计算该列的均值和标准差,然后将该列中的每个值减去均值并除以标准差。
将数据单位厘米,转成单位尺度,且满足均值为0,标准差为1。
# 标准化(均值为0,标准差为1)
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
第一步:特征分解——计算特征向量和特征值
第一种:特征分解
协方差矩阵(或相关矩阵)的特征向量和特征值代表PCA的“核心”:特征向量描述了数据的主要变化方向,而特征值则表示了在这些方向上的方差大小。
协方差矩阵
共p个特征,则计算得到的协方差矩阵为 p × p p×p p×p的方阵。
协方差矩阵计算公式
协方差矩阵 R R R:
R = [ r 11 r 12 ⋯ r 1 p r 21 r 22 ⋯ r 2 p ⋮ ⋮ ⋱ ⋮ r p 1 r p 2 ⋯ r p p ] R = \begin{bmatrix} r_{11} & r_{12} & \cdots & r_{1p} \\ r_{21} & r_{22} & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & r_{pp} \\ \end{bmatrix} R=
r11r21⋮rp1r12r22⋮rp2⋯⋯⋱⋯r1pr2p⋮rpp
两个特征 j、k 之间的协方差计算公式:
r j k = 1 n − 1 ∑ i = 1 n ( x i j − x ˉ j ) ( x i k − x ˉ k ) . r_{jk} = \frac{1}{n-1}\sum_{i=1}^{n}\left( x_{ij}-\bar{x}_j \right) \left( x_{ik}-\bar{x}_k \right). rjk=n−11i=1∑n(xij−xˉj)(xik−xˉk).
= 1 n − 1 ( ( X − x ˉ ) T ( X − x ˉ ) ) = \frac{1}{n-1} \left( (\mathbf{X} - \mathbf{\bar{x}})^T\;(\mathbf{X} - \mathbf{\bar{x}}) \right) =n−11((X−xˉ)T(X−xˉ))
其中, x ˉ \mathbf{\bar{x}} xˉ 是均值向量
x ˉ = 1 n ∑ i = 1 n x i . \mathbf{\bar{x}} = \frac{1}{n} \sum\limits_{i=1}^n x_{i}. xˉ=n1i=1∑nxi.
均值向量是⼀个p 维向量,其中该向量中的每个值代表数据集中特征列的样本均值。
计算协方差矩阵
# 计算协方差矩阵
import numpy as np
mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print('Covariance matrix \n%s' %cov_mat)
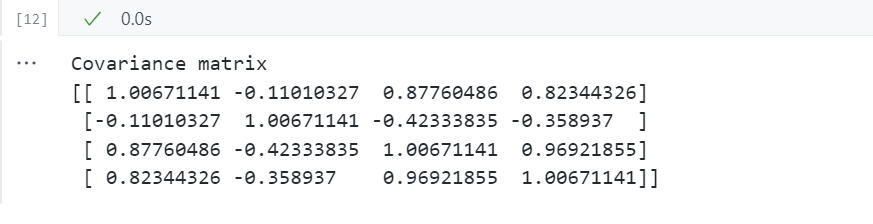
等价于np.cov
print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))
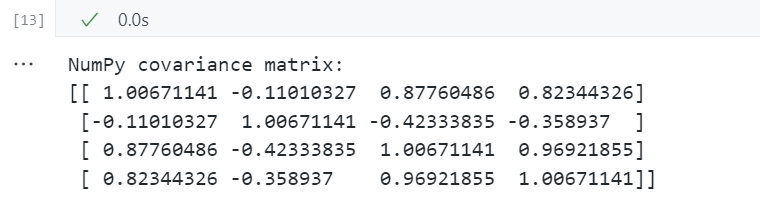
对协方差矩阵进行特征分解——计算特征向量、特征值
# 对协方差矩阵进行特征分解
cov_mat = np.cov(X_std.T) # 在标准化后的数据上,计算协方差矩阵
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
print('Eigenvectors \n%s' %eig_vecs) # 特征向量
print('\nEigenvalues \n%s' %eig_vals) # 特征值
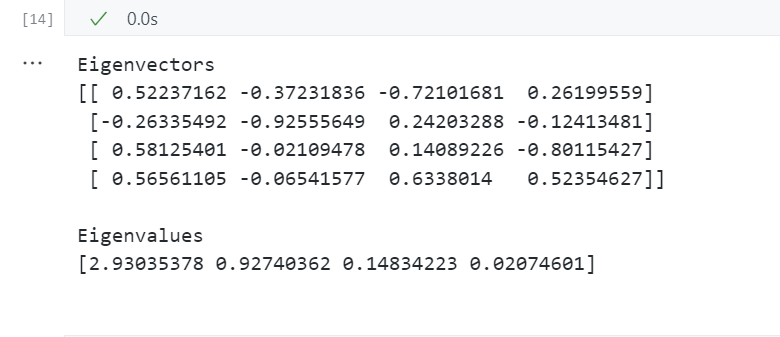
相关矩阵
特别是在“金融”领域,通常使用相关矩阵来代替协方差矩阵。但是,协方差矩阵的特征分解(如果输入数据已标准化)会产生与相关矩阵的特征分解相同的结果,因为相关矩阵可以理解为归一化的协方差矩阵。
对相关矩阵进行特征分解——计算特征向量、特征值
对标准化后的数据
# 对标准化后的数据计算相关矩阵并进行特征分解
cor_mat1 = np.corrcoef(X_std.T) # 对标准化后的数据计算相关矩阵
eig_vals, eig_vecs = np.linalg.eig(cor_mat1)
print('Eigenvectors \n%s' %eig_vecs) # 特征向量
print('\nEigenvalues \n%s' %eig_vals) # 特征值
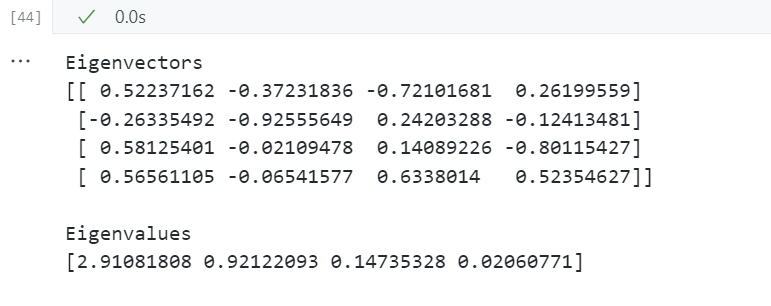
对原始数据
# 对原始数据计算相关矩阵并进行特征分解
cor_mat2 = np.corrcoef(X.T) # 对原始数据计算相关矩阵
eig_vals, eig_vecs = np.linalg.eig(cor_mat2)
print('Eigenvectors \n%s' %eig_vecs) # 特征向量
print('\nEigenvalues \n%s' %eig_vals) # 特征值
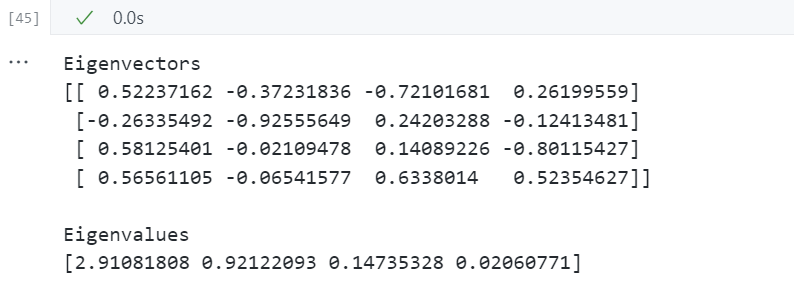
总结
以上三种方法的特征分解结果相同,即计算出的特征向量和特征值都一样:
数据标准化后协方差矩阵的特征分解;
数据标准化后相关矩阵的特征分解;
原始数据相关矩阵的特征分解。
第二种:奇异值分解SVD
PCA通过特征分解找到使方差最大化的正交基,实现数据的降维和特征提取。
然而,特征分解只适用于方阵(协方差矩阵为方阵),而现实中的数据矩阵往往不是方阵。这时,奇异值分解(SVD)就派上了用场。SVD是一种能适用于任意矩阵的分解方法,它并不要求分解的矩阵为方阵。
得到的左奇异矩阵 u u u是特征分解的特征向量;得到的奇异值 s s s与特征分解的特征值类似表示方差的大小。
# 奇异值分解SVD
u,s,v = np.linalg.svd(X_std.T)
u,s
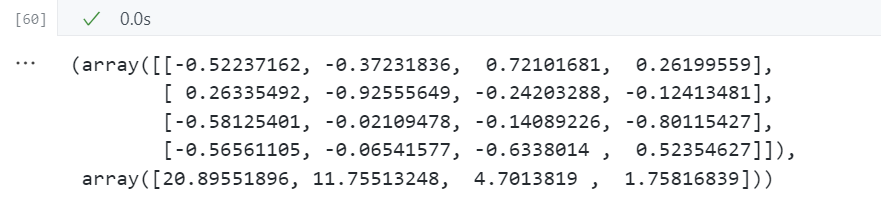
第二步:选择主成分
对特征进行排序
按降序对特征值进行排序,并选择 k k k个与最大特征值相对应的特征向量,其中 k k k是新特征子空间的维数( k ≤ p k≤p k≤p)
# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])
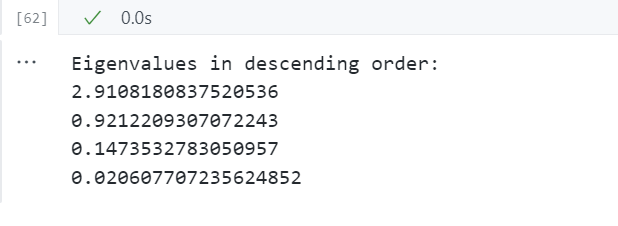
为新特征子空间选择多少个主成分(k值取多少)合适?
计算主成分贡献率及累计贡献率
第 i i i个主成分的贡献率, λ i \lambda_i λi代表第 i i i个特征向量的特征值:
λ i ∑ k = 1 p λ k \frac{\lambda_i}{\sum_{k=1}^{p}\lambda_k} ∑k=1pλkλi
前 i i i个主成分的累计贡献率:
∑ j = 1 i λ j ∑ k = 1 p λ k \frac{\sum_{j=1}^i{\lambda_j}}{\sum_{k=1}^{p}\lambda_k} ∑k=1pλk∑j=1iλj
一般取累计贡献率超过80%的特征值所对应的第一、第二、…、第m(m ≤ p)个主成分
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.figure(figsize=(6, 4))
plt.bar(range(4), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
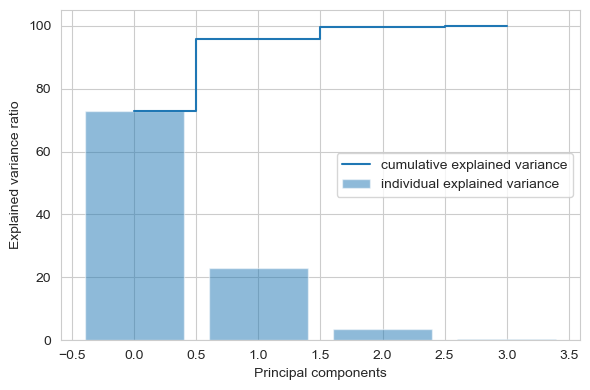
上图清楚地表明,大部分方差(准确地说是方差的72.77%)可以单独由第一个主成分来解释。第二个主成分仍然包含一些信息(23.03%),而第三和第四主成分可以安全地删除而不会丢失太多信息。前两个主成分合计包含95.8%的信息。
构建投影矩阵
将选择的 k k k个特征向量连接为投影矩阵 W W W,该矩阵用于将数据映射到新的特征子空间。
在这个例子里,选择具有最高特征值的前2个特征向量来构建我们的特征向量,将 4 维特征空间简化为 2 维特征子空间 p × k p×k p×k维投影矩阵 W W W。
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1)))
print('Matrix W:\n', matrix_w)
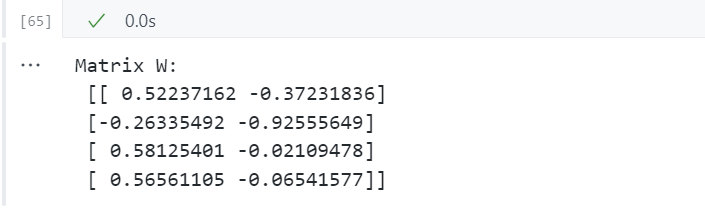
第三步:投影到新特征空间
通过投影矩阵 W W W对原始数据集 X X X进行变换,得到 k k k维特征子空间 Y Y Y。
在最后⼀步中,我们将使用4 × 2维投影矩阵 W W W通过方程 Y = X × W Y=X×W Y=X×W将样本转换到新的子空间,其中 Y Y Y是 150 × 2 150×2 150×2的矩阵。
Y = X_std.dot(matrix_w)
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
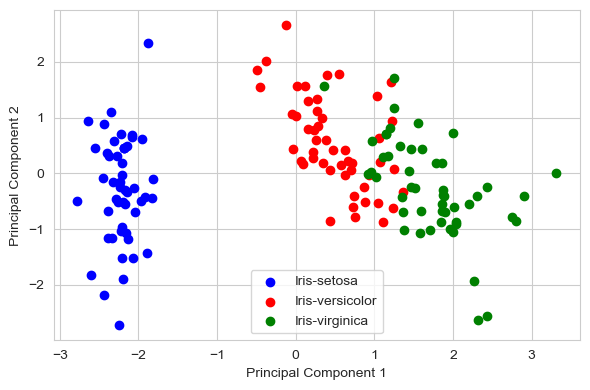
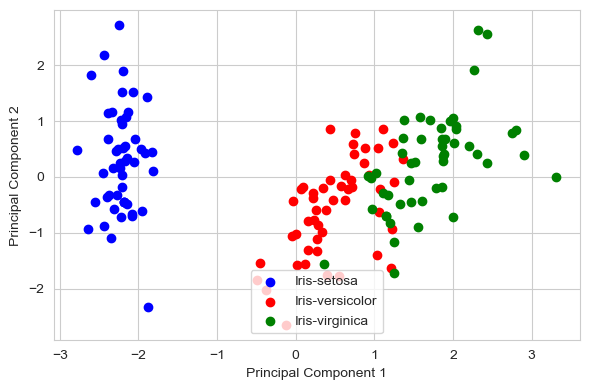
scikit-learn 库中的 PCA
from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2)
Y_sklearn = sklearn_pca.fit_transform(X_std)
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y_sklearn[y==lab, 0],
Y_sklearn[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
智能推荐
适合入门的8个趣味机器学习项目-程序员宅基地
文章浏览阅读86次。首发地址:https://yq.aliyun.com/articles/221708谈到机器学习,相信很多除学者都是通过斯坦福大学吴恩达老师的公开课《Machine Learning》开始具体的接触机器学习这个领域,但是学完之后又不知道自己的掌握情况,缺少一些实际的项目操作。对于机器学习的相关竞赛挑战,有些项目的门槛有些高,参加后难以具体的实现,因此造..._scrath五子棋下载
oracle 12c avg,Oracle 12c新特性系列专题-安徽Oracle授权认证中心-程序员宅基地
文章浏览阅读83次。原标题:Oracle 12c新特性系列专题-安徽Oracle授权认证中心 随着Oracle database 12c的普及,数据库管理员 (DBA) 的角色也随之发生了转变。 Oracle 12c数据库对 DBA 而言是下一代数据管理。它让 DBA 可以摆脱单调的日常管理任务,能够专注于如何从数据中获取更多价值。未来我们会推出基于Oracle12c的技术文章,帮助DBA尽快掌握新一代数据库的新特性..._ilm add policy row store compress advanced row after
第七周项目三(负数把正数赶出队列)-程序员宅基地
文章浏览阅读150次。问题及代码:*Copyright(c)2016,烟台大学计算机与控制工程学院 *All right reserved. *文件名称:负数把正数赶出队列.cpp *作者:张冰 *完成日期;2016年10月09日 *版本号;v1.0 * *问题描述: 设从键盘输入一整数序列a1,a2,…an,试编程实现: 当ai>0时,ai进队,当ai<0时,将队首元素出队,当ai
贪心+构造,LeetCode 1702. 修改后的最大二进制字符串-程序员宅基地
文章浏览阅读376次。贪心+构造
Linux命名空间学习教程(二) IPC-程序员宅基地
文章浏览阅读150次。本文讲的是Linux命名空间学习教程(二) IPC,【编者的话】Docker核心解决的问题是利用LXC来实现类似VM的功能,从而利用更加节省的硬件资源提供给用户更多的计算资源。而 LXC所实现的隔离性主要是来自内核的命名空间, 其中pid、net、ipc、mnt、uts 等命名空间将容器的进程、网络、消息、文件系统和hostname 隔离开。本文是Li..._主机的 ipc 命名空间
adb强制安装apk_adb绕过安装程序强制安装app-程序员宅基地
文章浏览阅读2w次,点赞5次,收藏7次。在设备上强制安装apk。在app已有的情况下使用-r参数在app版本低于现有版本使用-d参数命令adb install -r -d xxx.apk_adb绕过安装程序强制安装app
随便推点
STM32F407 越界问题定位_stm32flash地址越界怎么解决-程序员宅基地
文章浏览阅读290次。如果是越界进入硬件错误中断,MSP 或者 PSP 保存错误地址,跳转前会保存上一次执行的地址,lr 寄存器会保存子函数的地址,所以如果在 HardFault_CallBack 中直接调用 C 语言函数接口会间接修改了 lr,为了解决这个问题,直接绕过 lr 的 C 语言代码,用汇编语言提取 lr 寄存器再决定后面的操作。由于 STM32 加入了 FreeRTOS 操作系统,可能导致无法准确定位,仅供参考(日常编程需要考虑程序的健壮性,特别是对数组的访问,非常容易出现越界的情况)。_stm32flash地址越界怎么解决
利用SQL注入上传木马拿webshell-程序员宅基地
文章浏览阅读1.8k次。学到了一种操作,说实话,我从来没想过还能这样正常情况下,为了管理方便,许多管理员都会开放MySQL数据库的secure_file_priv,这时就可以导入或者导出数据当我如图输入时,就会在D盘创建一个名为123456.php,内容为<?php phpinfo();?>的文件我们可以利用这一点运用到SQL注入中,从拿下数据库到拿下目标的服务器比如我们在使用联合查询注入,正常是这样的语句http://xxx?id=-1 union select 1,'你想知道的字段的内容或查询语句',
Html CSS的三种链接方式_html链接css代码-程序员宅基地
文章浏览阅读2.9w次,点赞12次,收藏63次。感谢原文:https://blog.csdn.net/abc5382334/article/details/24260817感谢原文:https://blog.csdn.net/jiaqingge/article/details/52564348Html CSS的三种链接方式css文本的链接方式有三种:分别是内联定义、链入内部css、和链入外部css1.代码为:<html>..._html链接css代码
玩游戏哪款蓝牙耳机好?2021十大高音质游戏蓝牙耳机排名_适合游戏与运动的高音质蓝牙耳机-程序员宅基地
文章浏览阅读625次。近几年,蓝牙耳机市场发展迅速,越来越多的消费者希望抛弃线缆,更自由地听音乐,对于运动人士来说,蓝牙耳机的便携性显得尤为重要。但目前市面上的大多数蓝牙耳机实际上都是“有线”的,运动过程中产生的听诊器效应会严重影响听歌的感受。而在“真无线”耳机领域,除了苹果的AirPods外,可供选择的产品并不多,而AirPods又不是为运动场景打造的,防水能力非常差。那么对于喜欢运动又想要“自由”的朋友来说,有没有一款产品能够满足他们的需求呢?下面这十款小编专门为大家搜罗的蓝牙耳机或许就能找到适合的!网红击音F1_适合游戏与运动的高音质蓝牙耳机
iOS 17 测试版中 SwiftUI 视图首次显示时状态的改变导致动画“副作用”的解决方法-程序员宅基地
文章浏览阅读1k次,点赞6次,收藏7次。在本篇博文中,我们在 iOS 17 beta 4(SwiftUI 5.0)测试版中发现了 SwiftUI 视图首次显示时状态的改变会导致动画“副作用”的问题,并提出多种解决方案。
Flutter 自定义 轮播图的实现_flutter pageview轮播图 site:csdn.net-程序员宅基地
文章浏览阅读1.9k次。 在 上篇文章–Flutter 实现支持上拉加载和下拉刷新的 ListView 中,我们最终实现的效果是在 listView 上面留下了一段空白,本意是用来加载轮播图的,于是今天就开发了一下,希望能给各位灵感。一 、效果如下说一下大体思路 其实图片展示是用的 PageView ,然后,下面的指示器 是用的 TabPageSelector ,当然整体是用 Stack 包裹起来的。1、..._flutter pageview轮播图 site:csdn.net