深入理解快速傅里叶变换FFT-程序员宅基地
技术标签: FFT FFT理解 快速傅里叶变换 数字信号处理
深入理解快速傅里叶变换FFT
1.FFT介绍
\qquad 离散傅里叶变换(DFT)和卷积是信号处理中两个最基本也是最常用的运算,对于N点序列 x ( n ) x(n) x(n),其DFT变换对定义为:
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k k = 0 , 1 , 2 , . . . , N − 1 , W N = e − j 2 π N x ( n ) = 1 N ∑ k = 0 N − 1 X ( k ) W N − n k n = 0 , 1 , . . . , N − 1 \quad\quad\quad \quad X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad\quad k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi}{N}}\\ \quad \\ x(n)=\frac1N\sum_{k=0}^{N-1}X(k)W_N^{-nk} \quad\quad n=0,1,...,N-1 X(k)=n=0∑N−1x(n)WNnkk=0,1,2,...,N−1,WN=e−jN2πx(n)=N1k=0∑N−1X(k)WN−nkn=0,1,...,N−1
首先解释一下,这里的 W N = e − j 2 π N W_N=e^{-j\frac{2\pi}{N}} WN=e−jN2π是一个复数运算,其取得过程如下所示:
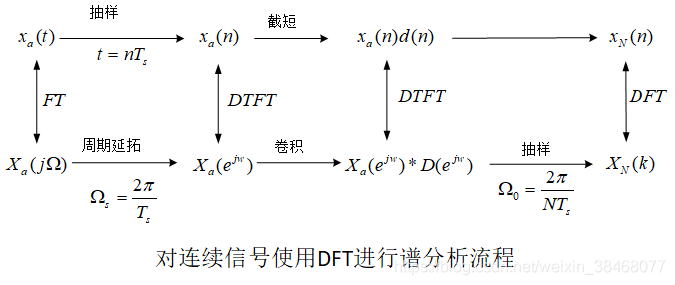
在上图中我们可以知道,这里的 W N W_N WN是经过截短了的。
\qquad 另外在上边的公式中,我们可以看出,由于 W N W_N WN是个复数,又因为k的取值范围在0到N-1,共有N个不同的选择,而对于每一个选定 k k k值的式子,其 n n n的取值范围又从0到N-1,由此可以算出,这 N N N个点 X ( k ) X(k) X(k)需要 N 2 N^2 N2次复数运算和 N ( N − 1 ) N(N-1) N(N−1)次复数加法。再由欧拉公式:
e j w = c o s w + j s i n w e − j w = c o s w − j s i n w e^{jw}=cosw+jsinw\\ \quad \\ e^{-jw}=cosw-jsinw ejw=cosw+jsinwe−jw=cosw−jsinw
将欧拉公式带入 W N W_N WN则有:
W N = e − j π 2 = c o s ( π 2 ) − j s i n ( π 2 ) = − j W_N=e^{-j\frac{\pi}{2}}=cos(\frac{\pi}{2})-jsin(\frac{\pi}{2})=-j WN=e−j2π=cos(2π)−jsin(2π)=−j
由以上公式则也可以分别求得 W N n k W_N^{nk} WNnk,当N等于4时,其表格如下所示:
| W N n k W_N^{nk} WNnk 取N=4 | Value |
|---|---|
| W N 0 W_N^0 WN0 | 1 1 1 |
| W N 1 W_N^1 WN1 | − j -j −j |
| W N 2 W_N^2 WN2 | − 1 -1 −1 |
| W N 3 W_N^3 WN3 | j j j |
| W N 4 W_N^4 WN4 | 1 1 1 |
| W N 6 W_N^6 WN6 | − 1 -1 −1 |
| W N 9 W_N^9 WN9 | − j -j −j |
在上边的运算中我们可以看到,虽然要运行的运算次数有很多,但是结果却是有一定规律的:
W N 0 = W N 4 = 1 W N 1 = W N 9 = − j W N 2 = W N 6 = − 1 W N 3 = j W_N^0=W_N^4=1\\ \quad \\ W_N^1=W_N^9=-j \\ \quad \\ W_N^2=W_N^6=-1\\ \quad \\ W_N^3=j WN0=WN4=1WN1=WN9=−jWN2=WN6=−1WN3=j
\qquad 到了这里,我们或许就看出来了一些规律,此处我们取的N=4,我们发现其结果也是以4为周期的。那么我们现在给出其一般性规律,也就是我们后边的进行快速FFT的基础。
W N 0 = 1 W N N / 2 = − 1 W N N + r = W N r W N ( N / 2 ) + r = − W N r W_N^0=1\\ \quad \\ W_N^{N/2}=-1\\ \quad \\ W_N^{N+r}=W_N^r\\ \quad \\ W_N^{(N/2)+r}=-W_N^r WN0=1WNN/2=−1WNN+r=WNrWN(N/2)+r=−WNr
\qquad 有了上边的规律,我们接下来就以4点DFT来测试一下,根据 X ( k ) X(k) X(k)的计算公式直接计算的话,我们则需要进行 4 2 = 16 4^2=16 42=16次的复数运算,所以我们根据以上得到的规律写成以下矩阵形式:
[ X ( 0 ) X ( 1 ) X ( 2 ) X ( 3 ) ] = [ 1 1 1 1 1 − j − 1 j 1 − 1 1 − 1 1 j − 1 − j ] [ x ( 0 ) x ( 1 ) x ( 2 ) x ( 3 ) ] \left[\begin{matrix} X(0)\\ X(1)\\X(2)\\X(3)\end{matrix}\right]= \left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -j & -1 & j \\ 1 & -1& 1 & -1 \\ 1 & j & -1 & -j \end{matrix} \right] \left[\begin{matrix} x(0)\\ x(1)\\x(2)\\x(3)\end{matrix}\right] ⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=⎣⎢⎢⎡11111−j−1j1−11−11j−1−j⎦⎥⎥⎤⎣⎢⎢⎡x(0)x(1)x(2)x(3)⎦⎥⎥⎤
\qquad 接下来我们就要对上边的矩阵进行一下初等变换,使得其结果仍然等于等式左侧(这里的对右边两个矩阵进行初等变换的目的是为了更加直观的显示出蝶形运算)。
为方便表示,我接下来分别将等式右边的矩阵定义为矩阵A和矩阵B,其形式如下:
A = [ 1 1 1 1 1 − j − 1 j 1 − 1 1 − 1 1 j − 1 − j ] B = [ x ( 0 ) x ( 1 ) x ( 2 ) x ( 3 ) ] A=\left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -j & -1 & j \\ 1 & -1& 1 & -1 \\ 1 & j & -1 & -j \end{matrix} \right] \qquad\qquad B=\left[\begin{matrix} x(0)\\ x(1)\\x(2)\\x(3)\end{matrix}\right] A=⎣⎢⎢⎡11111−j−1j1−11−11j−1−j⎦⎥⎥⎤B=⎣⎢⎢⎡x(0)x(1)x(2)x(3)⎦⎥⎥⎤
因为矩阵 A B = A E B AB=AEB AB=AEB,则上边的 X ( k ) X(k) X(k)的矩阵即可表示成:
[ X ( 0 ) X ( 1 ) X ( 2 ) X ( 3 ) ] = A [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] B = A [ 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ] [ 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ] B = [ 1 1 1 1 1 − 1 − j j 1 1 − 1 − 1 1 − 1 j − j ] [ x ( 0 ) x ( 2 ) x ( 1 ) x ( 3 ) ] \left[\begin{matrix} X(0)\\ X(1)\\X(2)\\X(3)\end{matrix}\right]=A\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0& 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]B \\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad =A\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1& 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1& 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]B \\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad =\left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -1 & -j & j \\ 1 & 1& -1 & -1 \\ 1 & -1 & j & -j \end{matrix} \right] \left[\begin{matrix} x(0)\\ x(2)\\x(1)\\x(3)\end{matrix}\right] ⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=A⎣⎢⎢⎡1000010000100001⎦⎥⎥⎤B=A⎣⎢⎢⎡1000001001000001⎦⎥⎥⎤⎣⎢⎢⎡1000001001000001⎦⎥⎥⎤B=⎣⎢⎢⎡11111−11−11−j−1j1j−1−j⎦⎥⎥⎤⎣⎢⎢⎡x(0)x(2)x(1)x(3)⎦⎥⎥⎤
\qquad 在上式中,我们对于矩阵A的第二列和第三列互换,将矩阵B的第二行和第三行互换,其结果不变。根据此结果,我们就可以的得出,如下等式:
X ( 0 ) = [ x ( 0 ) + x ( 2 ) ] + [ x ( 1 ) + x ( 3 ) ] X ( 1 ) = [ x ( 0 ) − x ( 2 ) ] − [ x ( 1 ) − x ( 3 ) ] j X ( 2 ) = [ x ( 0 ) + x ( 2 ) ] − [ x ( 1 ) + x ( 3 ) ] X ( 3 ) = [ x ( 0 ) − x ( 2 ) ] + [ x ( 1 ) − x ( 3 ) ] j X(0)=[x(0)+x(2)]+[x(1)+x(3)] \\ \quad \\ X(1)=[x(0)-x(2)]-[x(1)-x(3)]j\\ \quad \\ X(2)=[x(0)+x(2)]-[x(1)+x(3)]\\ \quad \\ X(3)=[x(0)-x(2)]+[x(1)-x(3)]j X(0)=[x(0)+x(2)]+[x(1)+x(3)]X(1)=[x(0)−x(2)]−[x(1)−x(3)]jX(2)=[x(0)+x(2)]−[x(1)+x(3)]X(3)=[x(0)−x(2)]+[x(1)−x(3)]j
\qquad 这样,四点DFT实际上只需要进行一次复数乘法,也就是只需要进行计算 [ x ( 1 ) − x ( 3 ) ] j [x(1)-x(3)]j [x(1)−x(3)]j即可,其实该问题的关键就是如何巧妙的利用W因子的周期性以及对称性,导出一个高效的快速算法。
\qquad 在上边的推导中,我们也可以看到在应用了快速傅里叶变换算法(FFT)后,使得N点的DFT算法的乘法计算量由 N 2 N^2 N2次运算降为 N 2 l o g 2 N \frac{N}{2}log_2N 2Nlog2N次,大大加快了计算速度。
2.时间抽取(DIT)基2 FFT算法
在介绍这个之前,我先介绍一下FFT的核心思想:

对于N点的DFT算法,我们习惯上使用 N = 2 M N=2^M N=2M来进行计算,根据DFT正变换的公式:
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k k = 0 , 1 , 2 , . . . , N − 1 , W N = e − j 2 π N X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad\quad k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi}{N}} X(k)=n=0∑N−1x(n)WNnkk=0,1,2,...,N−1,WN=e−jN2π
中我们将 x ( n ) x(n) x(n)分为奇、偶两部分,也就是令 n = 2 r 、 n = 2 r + 1 r = 0.1 , . . . , N 2 − 1 n=2r 、n=2r+1 \qquad r=0.1,..., \frac{N}{2}-1 n=2r、n=2r+1r=0.1,...,2N−1于是上式也就可以改写为:
X ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N 2 r k + ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N ( 2 r + 1 ) k = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N / 2 2 r k + ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N / 2 ( 2 r + 1 ) k X(k)=\sum_{r=0}^{N/2-1}x(2r)W_N^{2rk}+ \sum_{r=0}^{N/2-1}x(2r+1)W_N^{(2r+1)k}\\ \quad \\\quad\quad\quad =\sum_{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk}+ \sum_{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k} X(k)=r=0∑N/2−1x(2r)WN2rk+r=0∑N/2−1x(2r+1)WN(2r+1)k=r=0∑N/2−1x(2r)WN/22rk+r=0∑N/2−1x(2r+1)WN/2(2r+1)k
式中 W N / 2 = e − j 2 π N / 2 = e − j π W_{N/2}=e^{-j\frac{2\pi}{N/2}}=e^{-j\pi} WN/2=e−jN/22π=e−jπ
现在令 A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k):分别代表 X ( k ) X(k) X(k)的偶数项和奇数项:
A ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N / 2 2 r k k = 0 , 1 , . . . , N 2 − 1 B ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N / 2 ( 2 r + 1 ) k k = 0 , 1 , . . . , N 2 − 1 A(k)=\sum_{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk} \qquad k=0,1,...,\frac N2-1 \\ \quad \\\quad\quad\quad B(k)=\sum_{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k}\qquad k=0,1,...,\frac N2-1 \\ \quad \\ A(k)=r=0∑N/2−1x(2r)WN/22rkk=0,1,...,2N−1B(k)=r=0∑N/2−1x(2r+1)WN/2(2r+1)kk=0,1,...,2N−1
那么, X ( k ) X(k) X(k)则可以表示为:
X ( k ) = A ( k ) + W N k B ( k ) , k = 0 , 1 , . . . , N 2 − 1 X(k)=A(k)+W_N^kB(k),\qquad k=0,1,...,\frac N2-1 X(k)=A(k)+WNkB(k),k=0,1,...,2N−1
\qquad 但是此时我们仅可以根据该式子,算出来一半的 X ( k ) X(k) X(k),也就是 X ( 0 ) 、 X ( 1 ) X(0)、X(1) X(0)、X(1),而其余两项该式是无法求出的。具体的想要求出其余两项则需要公式:
X ( k + N 2 ) = A ( k + N 2 ) + W N k + N 2 B ( k + N 2 ) = A ( k + N 2 ) − W N k B ( k + N 2 ) = A ( k ) − W N k B ( k ) , k = 0 , 1 , . . . , N 2 − 1 X(k+\frac N2)=A(k+\frac N2)+W_N^{k+\frac N2}B(k+\frac N2)\\ \quad \\\quad\quad\quad\quad =A(k+\frac N2)-W_N^{k}B(k+\frac N2)\\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad = A(k)-W_N^{k}B(k)\quad ,k=0,1,...,\frac N2-1 X(k+2N)=A(k+2N)+WNk+2NB(k+2N)=A(k+2N)−WNkB(k+2N)=A(k)−WNkB(k),k=0,1,...,2N−1
\qquad 此处的 A ( k + N 2 ) A(k+\frac N2) A(k+2N)可以理解为偶数项的下一个周期,所以此处可以直接看为 A ( k ) A(k) A(k)。
所以用 A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k)可以完整的表示 X ( k ) X(k) X(k),当N=4时, A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k)以及 X ( k ) X(k) X(k)的关系如下所示:
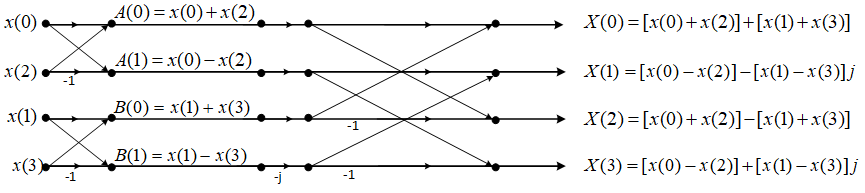
\qquad 这里我只展示了当N=4的时候,当N=8的时候,则我们需要继续将 A ( k ) A(k) A(k)分为偶数项 C ( k ) C(k) C(k)与奇数项 D ( k ) D(k) D(k)之和,将 B ( k ) B(k) B(k)分为偶数项 E ( k ) E(k) E(k)与奇数项 F ( k ) F(k) F(k)之和,其 k k k值取值范围为 k = 0 , 1 , . . . , N 4 − 1 k=0,1,...,\frac N4-1 k=0,1,...,4N−1。
\qquad 若N=16,或者更高的幂,可以按照这样的方法继续分下去,直到分到两点的DFT为止。
介绍到这里,相信大家都已经很明白了,该算法是将时间 n n n按照奇、偶分开,所以被称为时间抽取算法。
3.FFT算法的一般规律
\qquad 我们知道,对于进行FFT快速傅里叶变换,找到W因子的周期性以及对称性是非常关键的。比如当N=4的时候, x ( 0 ) 、 x ( 1 ) 、 x ( 2 ) 、 x ( 3 ) x(0)、x(1)、x(2)、x(3) x(0)、x(1)、x(2)、x(3)的排列顺序为 x ( 0 ) 、 x ( 2 ) 、 x ( 1 ) 、 x ( 3 ) x(0)、x(2)、x(1)、x(3) x(0)、x(2)、x(1)、x(3)。如果这个顺序让我们自己取记忆的话,如果当N值小的时候或许还可以记住,但是如果当N大的时候,这样单纯记忆就显得不切实际。为此,我们能否找到它的排列规律显得尤为重要,以下我将分别以N=4和N=8来介绍这一方法:
当N=4时其表格如下:
| n n n | x ( n ) x(n) x(n) | X ( k ) X(k) X(k) | k k k |
|---|---|---|---|
| 0 | 00 | 000 | 0 |
| 2 | 10 | 001 | 1 |
| 1 | 01 | 010 | 2 |
| 3 | 11 | 011 | 3 |
当N=8时其表格如下:
| n n n | x ( n ) x(n) x(n) | X ( k ) X(k) X(k) | k k k |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 4 | 100 | 001 | 1 |
| 2 | 010 | 010 | 2 |
| 6 | 110 | 011 | 3 |
| 1 | 001 | 100 | 4 |
| 5 | 101 | 101 | 5 |
| 3 | 011 | 110 | 6 |
| 7 | 111 | 111 | 7 |
仔细观看的话,我们或许会发现 x ( n ) x(n) x(n)的取值顺序也是按照二进制加法,但是这个加法是在左侧加,而 X ( k ) X(k) X(k)则是在右侧加。也就是说是 X ( k ) X(k) X(k)的对称。有了这个规律,那么不管 N = 2 M N=2^M N=2M的值取多大,我们都可以快速的排列出其顺序,这对于加快运算速度是有很大帮助的。
因为 M = l o g 2 N M=log_2N M=log2N所以将N点DFT可以分成M级,当N等于8时,M=3,从左到右可以分为 m = 0 , m = 1 , m = 2 m=0,m=1,m=2 m=0,m=1,m=2三级。接下来我将展示8点DFT时间抽取算法的信号流图:
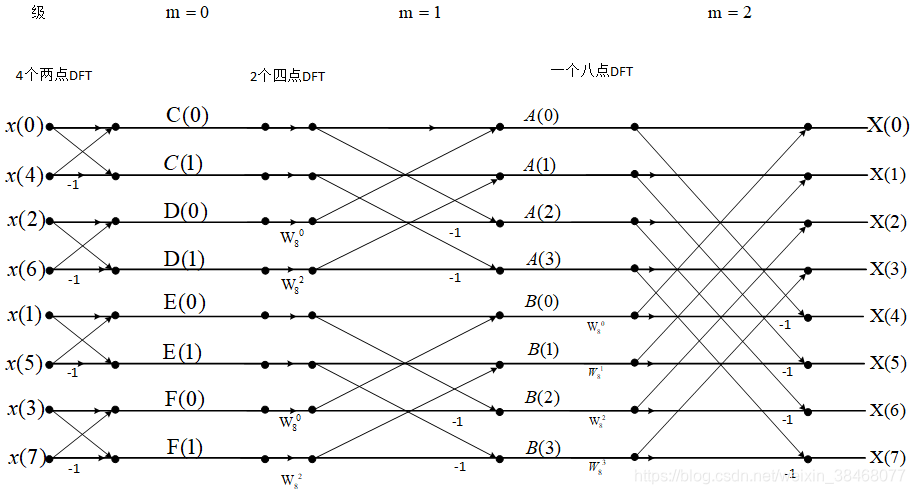
这里我们或许就会看到如下现象:
在每一个向上连接的线的下边都要乘一个 W r W^r Wr因子,
每一个向下连接的线的搭档都需要乘-1。
下面我将会来介绍一下 W r W^r Wr因子的分布情况:
| m m m 值(第几级) | 对应的 W r W^r Wr因子分布 |
|---|---|
| m = 0 m=0 m=0 级 | W 2 r , r = 0 W_2^r,r=0 W2r,r=0 |
| m = 1 m=1 m=1 级 | W 4 r , r = 0 , 1 W_4^r,r=0,1 W4r,r=0,1 |
| m = 2 m=2 m=2 级 | W 8 r , r = 0 , 1 , 2 , 3 W_8^r,r=0,1,2,3 W8r,r=0,1,2,3 |
| … | … |
| m = M − 1 m=M-1 m=M−1 级 | W N r , r = 0 , 1 , . . . , N 2 − 1 W_N^r,r=0,1,...,\frac N2-1 WNr,r=0,1,...,2N−1 |
如果你仔细看我的流图的话或许会发现,我在m=1的时候,使用了因子 W 8 0 , W 8 2 W_8^0,W_8^2 W80,W82,在这里我使用这个因子只是为了方便和后边的比较,其实这个还是有一个代换公式的:
W 8 0 = W 4 0 , W 8 2 = W 4 1 W_8^0=W_4^0,W_8^2=W_4^1 W80=W40,W82=W41
4.后续
该部分留作后边对于FFT的更加深入的理解。
智能推荐
攻防世界_难度8_happy_puzzle_攻防世界困难模式攻略图文-程序员宅基地
文章浏览阅读645次。这个肯定是末尾的IDAT了,因为IDAT必须要满了才会开始一下个IDAT,这个明显就是末尾的IDAT了。,对应下面的create_head()代码。,对应下面的create_tail()代码。不要考虑爆破,我已经试了一下,太多情况了。题目来源:UNCTF。_攻防世界困难模式攻略图文
达梦数据库的导出(备份)、导入_达梦数据库导入导出-程序员宅基地
文章浏览阅读2.9k次,点赞3次,收藏10次。偶尔会用到,记录、分享。1. 数据库导出1.1 切换到dmdba用户su - dmdba1.2 进入达梦数据库安装路径的bin目录,执行导库操作 导出语句:./dexp cwy_init/[email protected]:5236 file=cwy_init.dmp log=cwy_init_exp.log 注释: cwy_init/init_123..._达梦数据库导入导出
js引入kindeditor富文本编辑器的使用_kindeditor.js-程序员宅基地
文章浏览阅读1.9k次。1. 在官网上下载KindEditor文件,可以删掉不需要要到的jsp,asp,asp.net和php文件夹。接着把文件夹放到项目文件目录下。2. 修改html文件,在页面引入js文件:<script type="text/javascript" src="./kindeditor/kindeditor-all.js"></script><script type="text/javascript" src="./kindeditor/lang/zh-CN.js"_kindeditor.js
STM32学习过程记录11——基于STM32G431CBU6硬件SPI+DMA的高效WS2812B控制方法-程序员宅基地
文章浏览阅读2.3k次,点赞6次,收藏14次。SPI的详情简介不必赘述。假设我们通过SPI发送0xAA,我们的数据线就会变为10101010,通过修改不同的内容,即可修改SPI中0和1的持续时间。比如0xF0即为前半周期为高电平,后半周期为低电平的状态。在SPI的通信模式中,CPHA配置会影响该实验,下图展示了不同采样位置的SPI时序图[1]。CPOL = 0,CPHA = 1:CLK空闲状态 = 低电平,数据在下降沿采样,并在上升沿移出CPOL = 0,CPHA = 0:CLK空闲状态 = 低电平,数据在上升沿采样,并在下降沿移出。_stm32g431cbu6
计算机网络-数据链路层_接收方收到链路层数据后,使用crc检验后,余数为0,说明链路层的传输时可靠传输-程序员宅基地
文章浏览阅读1.2k次,点赞2次,收藏8次。数据链路层习题自测问题1.数据链路(即逻辑链路)与链路(即物理链路)有何区别?“电路接通了”与”数据链路接通了”的区别何在?2.数据链路层中的链路控制包括哪些功能?试讨论数据链路层做成可靠的链路层有哪些优点和缺点。3.网络适配器的作用是什么?网络适配器工作在哪一层?4.数据链路层的三个基本问题(帧定界、透明传输和差错检测)为什么都必须加以解决?5.如果在数据链路层不进行帧定界,会发生什么问题?6.PPP协议的主要特点是什么?为什么PPP不使用帧的编号?PPP适用于什么情况?为什么PPP协议不_接收方收到链路层数据后,使用crc检验后,余数为0,说明链路层的传输时可靠传输
软件测试工程师移民加拿大_无证移民,未受过软件工程师的教育(第1部分)-程序员宅基地
文章浏览阅读587次。软件测试工程师移民加拿大 无证移民,未受过软件工程师的教育(第1部分) (Undocumented Immigrant With No Education to Software Engineer(Part 1))Before I start, I want you to please bear with me on the way I write, I have very little gen...
随便推点
Thinkpad X250 secure boot failed 启动失败问题解决_安装完系统提示secureboot failure-程序员宅基地
文章浏览阅读304次。Thinkpad X250笔记本电脑,装的是FreeBSD,进入BIOS修改虚拟化配置(其后可能是误设置了安全开机),保存退出后系统无法启动,显示:secure boot failed ,把自己惊出一身冷汗,因为这台笔记本刚好还没开始做备份.....根据错误提示,到bios里面去找相关配置,在Security里面找到了Secure Boot选项,发现果然被设置为Enabled,将其修改为Disabled ,再开机,终于正常启动了。_安装完系统提示secureboot failure
C++如何做字符串分割(5种方法)_c++ 字符串分割-程序员宅基地
文章浏览阅读10w+次,点赞93次,收藏352次。1、用strtok函数进行字符串分割原型: char *strtok(char *str, const char *delim);功能:分解字符串为一组字符串。参数说明:str为要分解的字符串,delim为分隔符字符串。返回值:从str开头开始的一个个被分割的串。当没有被分割的串时则返回NULL。其它:strtok函数线程不安全,可以使用strtok_r替代。示例://借助strtok实现split#include <string.h>#include <stdio.h&_c++ 字符串分割
2013第四届蓝桥杯 C/C++本科A组 真题答案解析_2013年第四届c a组蓝桥杯省赛真题解答-程序员宅基地
文章浏览阅读2.3k次。1 .高斯日记 大数学家高斯有个好习惯:无论如何都要记日记。他的日记有个与众不同的地方,他从不注明年月日,而是用一个整数代替,比如:4210后来人们知道,那个整数就是日期,它表示那一天是高斯出生后的第几天。这或许也是个好习惯,它时时刻刻提醒着主人:日子又过去一天,还有多少时光可以用于浪费呢?高斯出生于:1777年4月30日。在高斯发现的一个重要定理的日记_2013年第四届c a组蓝桥杯省赛真题解答
基于供需算法优化的核极限学习机(KELM)分类算法-程序员宅基地
文章浏览阅读851次,点赞17次,收藏22次。摘要:本文利用供需算法对核极限学习机(KELM)进行优化,并用于分类。
metasploitable2渗透测试_metasploitable2怎么进入-程序员宅基地
文章浏览阅读1.1k次。一、系统弱密码登录1、在kali上执行命令行telnet 192.168.26.1292、Login和password都输入msfadmin3、登录成功,进入系统4、测试如下:二、MySQL弱密码登录:1、在kali上执行mysql –h 192.168.26.129 –u root2、登录成功,进入MySQL系统3、测试效果:三、PostgreSQL弱密码登录1、在Kali上执行psql -h 192.168.26.129 –U post..._metasploitable2怎么进入
Python学习之路:从入门到精通的指南_python人工智能开发从入门到精通pdf-程序员宅基地
文章浏览阅读257次。本文将为初学者提供Python学习的详细指南,从Python的历史、基础语法和数据类型到面向对象编程、模块和库的使用。通过本文,您将能够掌握Python编程的核心概念,为今后的编程学习和实践打下坚实基础。_python人工智能开发从入门到精通pdf