一阶卡尔曼（无详细推导，初步认识原理）

字符定义

${\hat{X}}_k$表示第k次估计值（上面的 $\hat{}$ 号表示估计）
$Z_k$表示第k次测量值
$K_k$表示第k次得到的卡尔曼系数
$e_{ES{T}_k}$表示第k次估计误差
$e_{ME{A}_k}$表示第k次测量误差

递归算法

如果我们想要得到某个数据时，可以通过测量获得。但测量总是存在误差的。比如我们想要知道一本书的厚度，可以用尺子进行测量，而尺子上的量程是毫米，所以我们最多只能得到精确到毫米的厚度。如果书厚度的真实值是10.49mm，那么我们的测量值大概就是10mm或者11mm，这时候测量值与书厚度的真实值就存在误差了。
这时我们可以通过多次测量求平均来得到一个相对准确的估计值，用式子表示就是：
$${\hat{X}}_k=\frac{Z_1+Z_2+...+Z_k}{k}$$
当我们测量的次数一多时，需要记录的测量值也变多，有什么方法可以减少需要记录下的测量值吗？这时我们可以继续简单推导就可得：
$$\begin{array}{rl}{\hat{X}}_k& =\frac{1}{k}\times (Z_1+Z_2+...+Z_k)\\ & =\frac{1}{k}\times (Z_1+Z_2+...+Z_{k-1})+\frac{1}{k}\times Z_k\\ & =\frac{k-1}{k}\times [\frac{1}{k-1}\times (Z_1+Z_2+...+Z_{k-1})]+\frac{1}{k}\times Z_k\\ & =\frac{k-1}{k}\times {\hat{X}}_{k-1}+\frac{1}{k}\times Z_k\\ & ={\hat{X}}_{k-1}+\frac{1}{k}\times (Z_k-{\hat{X}}_{k-1})\end{array}$$
这时我们每次计算当前估计值${\hat{X}}_k$就只需要上一次估计值$\widehat{X_{k-1}}$、当前测量值$Z_k$，而不是所有的测量值。
令卡尔曼系数$K_k=\frac{1}{k}$，我们就得到了一阶卡尔曼滤波的第一条基本公式
$${\hat{X}}_k={\hat{X}}_{k-1}+K_k\times (Z_k-{\hat{X}}_{k-1})\text{\hspace{1em}(1-1)}$$

一阶卡尔曼系数

对于式1-1，我们清楚地知道${\hat{X}}_k$是估计值，$Z_k$是测量值，那么$K_k$表示什么呢？
我们先不进行推导直接给出两条式子（推导会在卡尔曼增益详细推导中给出）。
$$K_k=\frac{e_{ES{T}_{k-1}}}{e_{ES{T}_{k-1}}+e_{ME{A}_k}}\text{\hspace{1em}(1-2)}$$
$$e_{ES{T}_k}=(1-K_k)\times e_{ES{T}_{k-1}}\text{\hspace{1em}(1-3)}$$
由式1-2可知：
当估计误差远远大于计算误差，即$e_{ES{T}_k}>>e_{ME{A}_k}$时，$K_k=1$，${\hat{X}}_k=Z_k$；
当估计误差远远小于计算误差，即$e_{ES{T}_k}<<e_{ME{A}_k}$时，$K_k=0$，${\hat{X}}_k={\hat{X}}_{k-1}$。
这时我们就可以大概看出卡尔曼系数$K_k$的意义，
当估计误差大，测量误差小时，卡尔曼系数就越接近1，我们的计算结果就接近测量值；
当估计误差小，测量误差大时，卡尔曼系数就越接近0，我们的计算结果就接近估计值。
所以卡尔曼系数表示的是对测量值的信任程度。
从实际来说也是特别好理解的，
当我们测量的值越准时，卡尔曼系数就越接近1，我们就越相信测量值；
当我们估计的值越准时，卡尔曼系数就越接近0，我们就越不相信测量值。

一阶卡尔曼滤波器的简单使用

使用一阶卡尔曼滤波器需要进行三个步骤，然后不断重复这三个步骤即可。
$$\begin{array}{rl}step1& 计算卡尔曼系数K_k=\frac{e_{ES{T}_{k-1}}}{e_{ES{T}_{k-1}}+e_{ME{A}_k}}\\ step2& 计算估计值{\hat{X}}_k={\hat{X}}_{k-1}+K_k\times (Z_k-{\hat{X}}_{k-1})\\ step3& 更新估计误差e_{ES{T}_k}=(1-K_k)\times e_{ES{T}_{k-1}}\end{array}$$
我们知道用同一测量工具测量时，测量误差是不用变的。而当我们的估计模型改变时，估计误差也改变了。一阶卡尔曼滤波器的估计模型就是step2的公式。
第一步，我们根据测量误差与估计误差确定卡尔曼系数，从而确定一个一阶卡尔曼滤波器的模型。
第二步，我们利用新模型和新的测量值计算出新的估计值。
第三步，我们用新的卡尔曼系数来更新新模型的估计误差。
然后不断循环，使用模型越来越合适。
例子：假设我们测量一个桌子的高度，真实值是500cm，测量误差是10cm（也就是说测量值在490cm到510cm之间任意取值），我们假设最开始的估计值为400cm，估计误差为120cm（估计值和估计误差可以任意取值，因为从上面那三个步骤我们可以知道估计值和估计误差会随着计算而自动改变）。
我用excel得：

其中可以调整的数据为测量误差，首个估计误差，首个估计值。虽然测量值是随机的，可以改变，但并不算我们研究的范围。
接下来给出不同初始值，相同测量值的图，然后大家自己分析不同的原因。
测量误差：10，首个估计误差：120，首个估计值：400。

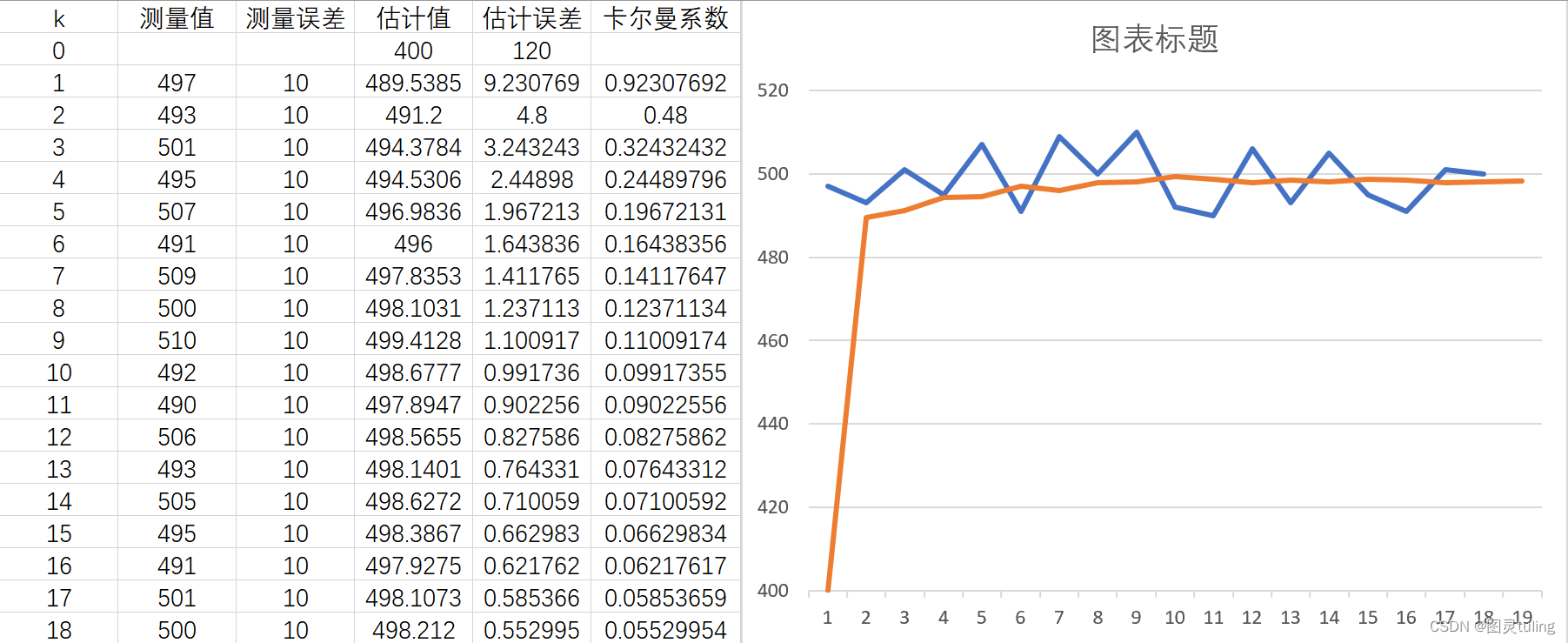
测量误差：100，首个估计误差：120，首个估计值：400。

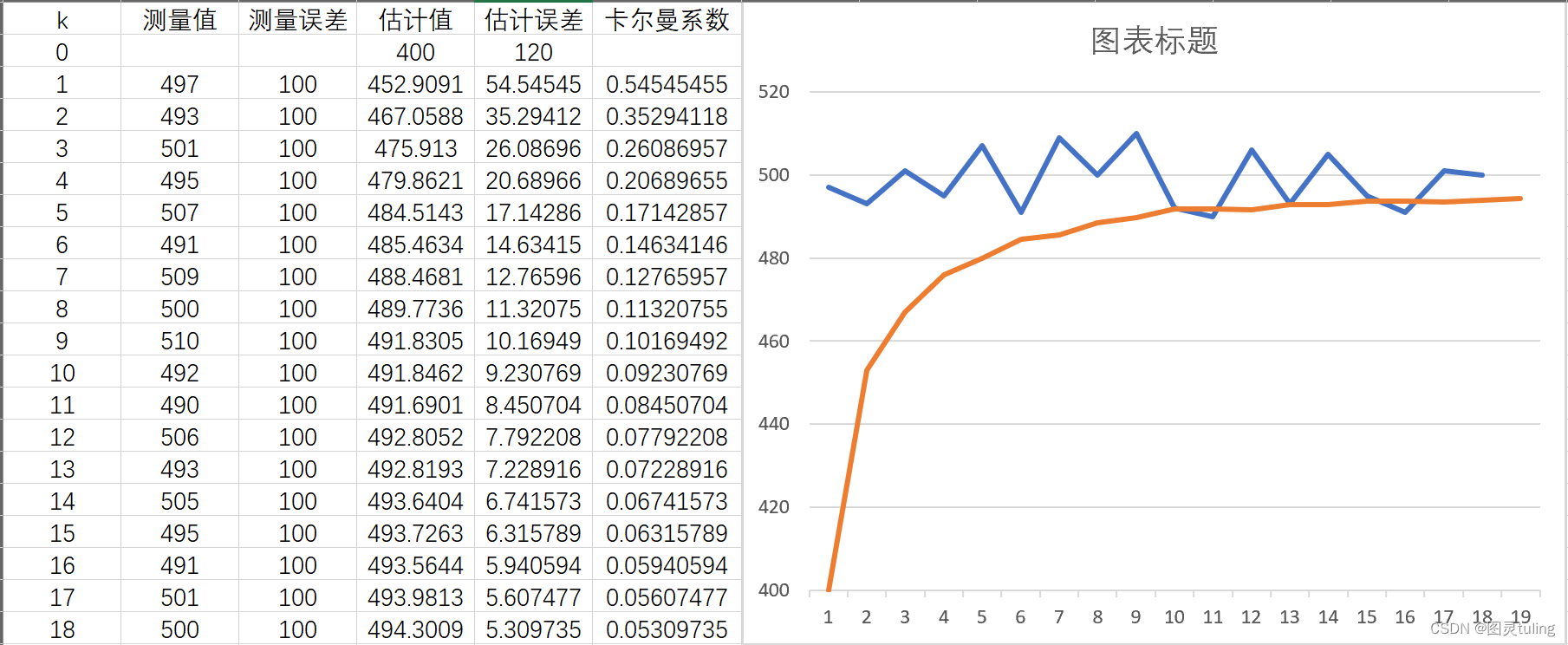
测量误差：10，首个估计误差：12，首个估计值：400。

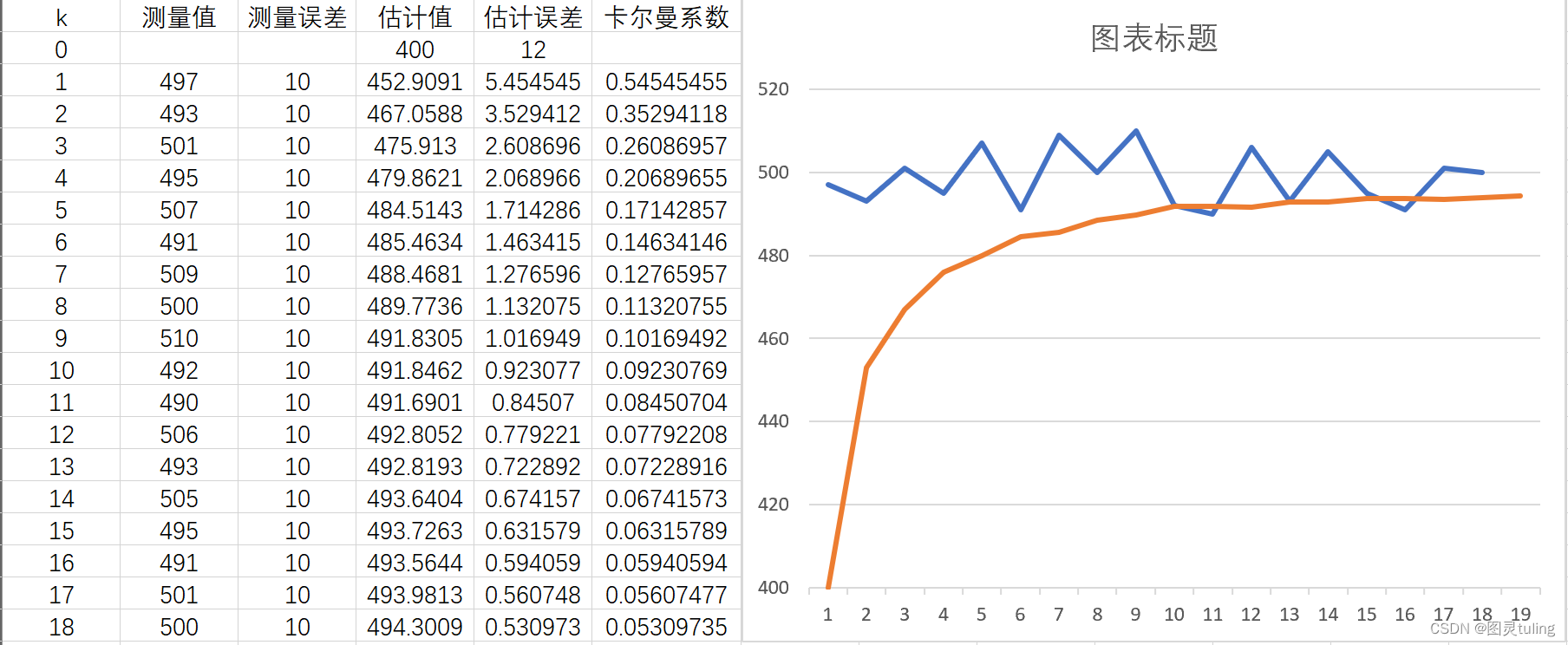
测量误差：10，首个估计误差：120，首个估计值：600。

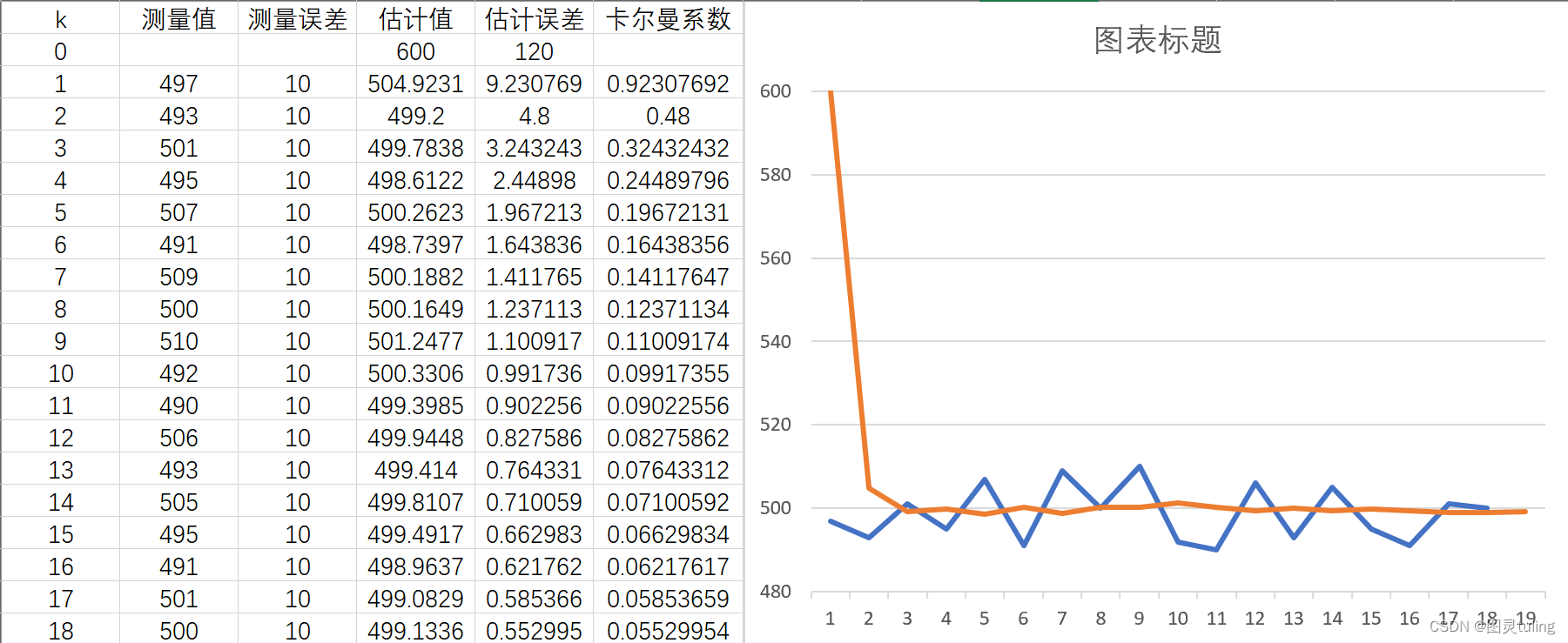
测量误差：10，首个估计误差：120，首个估计值：500。

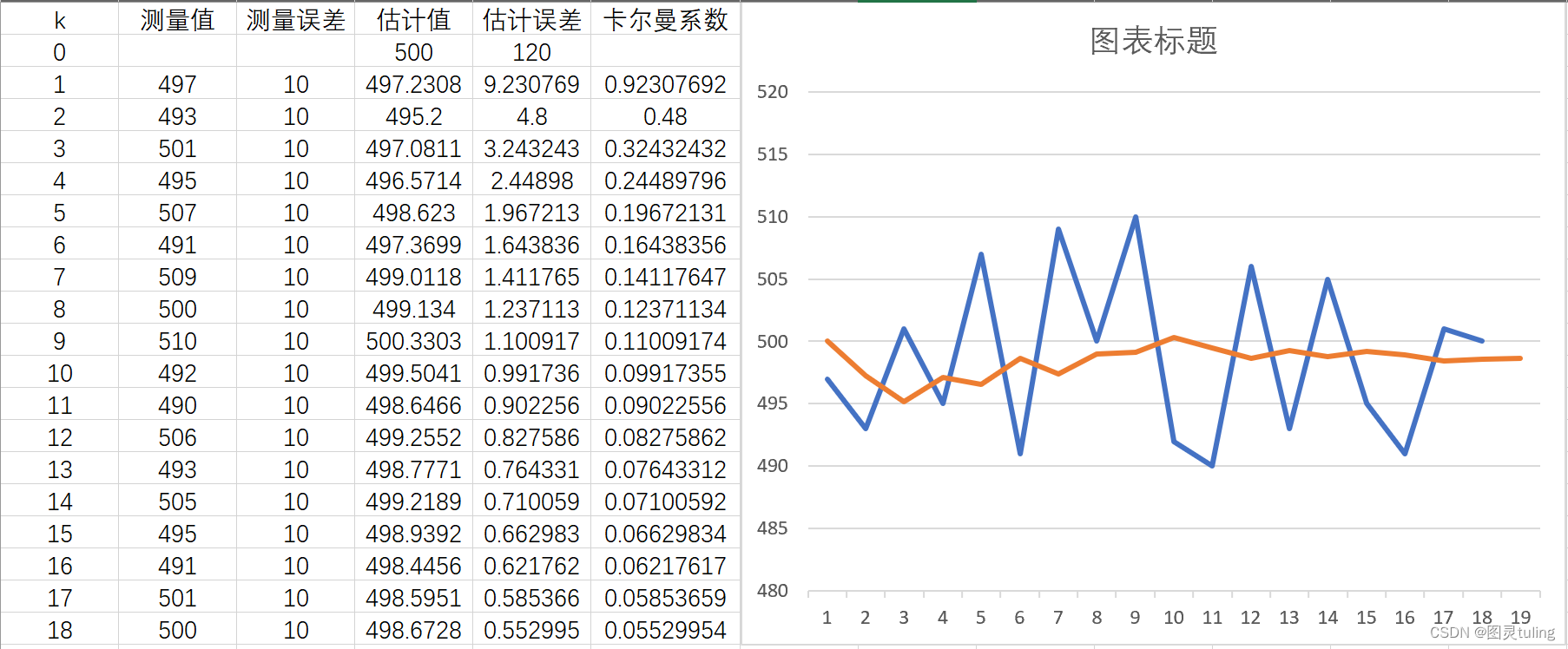
可以看出，不管如何，估计值最终都会逼近真实值，只是响应不同的区别而已。

卡尔曼滤波（矩阵运算，详细推导）

前置知识

这里简单介绍给出概念，想要真正学会这些前置知识需要查找其它资料深入学习。
且后继的所有变量几乎都是矩阵，还需要进行概率运算，所以需要拥有一定的概率论和线性代数基础。

数据融合

数据融合，大概就是把一系列原始数据进行处理，最后得到一个更加优化的数据。一阶卡尔曼的第一条基本公式${\hat{X}}_k={\hat{X}}_{k-1}+K_k\times (Z_k-{\hat{X}}_{k-1})$就可以对两个数据进行融合，不过它需要变化一下，变为：
$$\hat{X}=Z_1+K_k\times (Z_2-Z_1)$$
其中$\hat{X}$为融合后的数据（估计值），$Z_1$，$Z_2$为融合前的原始数据，$K_k$来控制如何融合（由融合目标推出）。
比如：我们用两个测试工具来测试一个鸡蛋的重量，其中一个测得45g，它的测量误差服从正态分布，方差${\sigma }_1$为3g，另一个测得47g，它的测量误差也服从正态分布，方差${\sigma }_2$为2g。
现在就是已知$Z_1=45$，$Z_2=47$，${\sigma }_1=3$，${\sigma }_2=2$，要求一个更为准确的重量$\hat{X}$，目标为更加准确（即方差最小）。
所以得$D(\hat{X})=D(Z_1+K_k\times (Z_2-Z_1))$
$Z_1$与$Z_2$相互独立，所以$D(\hat{X})=D(Z_1+K_k\times (Z_2-Z_1))$
$$\begin{array}{rl}D(\hat{X})& =D(Z_1\times (1-K_k)+Z_2\times K_k)\\ & =D(Z_1\times (1-K_k))+D(Z_2\times K_k)\\ & =(1-K_k{)}^{2}D(Z_1)+K_k^{2}D(Z_2)\\ & =(1-K_k{)}^2{\sigma }_1^2+K_k^2{\sigma }_2^2\end{array}$$
我们要通过改变$K_k$使得$D(\hat{X})$最小，所以$D(\hat{X})$对$K_k$求导，算出极值点。
$$\frac{dD(\hat{X})}{d{K}_k}=-2(1-K_k){\sigma }_1^2+2{\sigma }_2^2{K}_k=0$$
解得$K_k=\frac{{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}\approx 0.69$
故$$\begin{gathered} \hat{X}=Z_1+K_k\times (Z_2-Z_1)\approx 46.385g \\ {\sigma }_x=\sqrt{D(\hat{X})}=\sqrt{(1-K_k{)}^2{\sigma }_1^2+K_k^2{\sigma }_2^2}\approx 1.67g \end{gathered}$$
求解完成，我们用两个有误差的数据进行数据融合，获得了一个误差更小的数据。

协方差矩阵

协方差矩阵就是把方差和协方差在一个矩阵中表示出来，体现变量之间的关系。
比如我们有三组变量$x_i,y_i,z_i$，具体如下：

i	x	y	z
1	179	74	33
2	187	80	31
3	175	71	28

可得$$\begin{gathered} \bar{x}=180.3,\bar{y}=75,\bar{z}=30.7 \\ {\sigma }_x^2=\frac{1}{3}((x_1-\bar{x}{)}^2+(x_2-\bar{x}{)}^2+(x_3-\bar{x}{)}^2)=24.89 \\ {\sigma }_y^2=\frac{1}{3}((y_1-\bar{y}{)}^2+(y_2-\bar{y}{)}^2+(y_3-\bar{y}{)}^2)=14 \\ {\sigma }_z^2=\frac{1}{3}((z_1-\bar{z}{)}^2+(z_2-\bar{z}{)}^2+(z_3-\bar{z}{)}^2)=4.22 \\ {\sigma }_x{\sigma }_y={\sigma }_y{\sigma }_x=\frac{1}{3}((x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+(x_3-\bar{x})(y_3-\bar{y})=18.7 \\ {\sigma }_x{\sigma }_z={\sigma }_z{\sigma }_x=\frac{1}{3}((x_1-\bar{x})(z_1-\bar{z})+(x_2-\bar{x})(z_2-\bar{z})+(x_3-\bar{x})(z_3-\bar{z})=4.4 \\ {\sigma }_y{\sigma }_z={\sigma }_z{\sigma }_y=\frac{1}{3}((y_1-\bar{y})(z_1-\bar{z})+(y_2-\bar{y})(z_2-\bar{z})+(y_3-\bar{y})(z_3-\bar{z})=3.3 \end{gathered}$$
所以这三组数据的协方差矩阵为
$$P=\left[\begin{array}{ccc}{\sigma }_x^2& {\sigma }_y{\sigma }_x& {\sigma }_z{\sigma }_x\\ {\sigma }_x{\sigma }_y& {\sigma }_y^2& {\sigma }_z{\sigma }_y\\ {\sigma }_x{\sigma }_z& {\sigma }_y{\sigma }_z& {\sigma }_z^2\end{array}\right]=\left[\begin{array}{ccc}24.89& 18.7& 4.4\\ 18.7& 14& 3.3\\ 4.4& 3.3& 4.22\end{array}\right]$$
其中，以${\sigma }_x{\sigma }_y$就表示变量x与变量y的线性关系程度，越趋近$+\infty$就越正相关，越趋近$-\infty$就越负相关，越趋近0就越无线性关系。但不同协方差之间不能比较，比如不能因为${\sigma }_x{\sigma }_y>{\sigma }_x{\sigma }_z$就说变量x与y的线性关系比x与z的线性关系强，因为这与变量值的大小有关，可以用计算式子看出来。
最终我们可以求协方差矩阵的通用式子：
如果存在一个数据矩阵$\left[\begin{array}{cccc}{x}_1& y_1& z_1& ...\\ x_2& y_2& z_2& ...\\ ...& ...& ...& ...\\ x_n& y_n& z_n& ...\end{array}\right]$
则有过渡矩阵$a=\left[\begin{array}{cccc}{x}_1& y_1& z_1& ...\\ x_2& y_2& z_2& ...\\ ...& ...& ...& ...\\ x_n& y_n& z_n& ...\end{array}\right]-\frac{1}{3}\left[\begin{array}{cccc}1& 1& 1& ...\\ 1& 1& 1& ...\\ ...& ...& ...& ...\\ 1& 1& 1& ...\end{array}\right]\left[\begin{array}{cccc}{x}_1& y_1& z_1& ...\\ x_2& y_2& z_2& ...\\ ...& ...& ...& ...\\ x_n& y_n& z_n& ...\end{array}\right]$
（所有元素全为1的矩阵与数据矩阵大小相同，过渡矩阵就是数据矩阵减去它的平均值，相当于$x_i-\bar{x}$）
则这个数据矩阵的协方差矩阵为
$$P=\frac{1}{3}{a}^{T}a(a^T为a的转置)$$
可以用上面的例子自己一步一步计算体验一下，最终得到的协方差矩阵是一样的。

状态空间方程

我们以一个简单的弹簧振动阻尼系统为例：

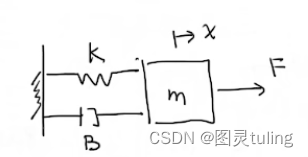
向右为x轴正方向，弹簧胡克系数为k，阻尼系数为B(可理解为与空气阻力有关的系数)，物体质量为m，对物体施加的力为F。
我们可以得到$m\ddot{x}+B\dot{x}+kx=F=u$，其中$\dot{x}$为$x$的一阶导，$F$可以理解为对这个系统的输入(input)，即$u$
我们可以设两个状态变量$x_1,x_2$分别位置，速度，得：
$$\begin{gathered} x_1=x \\ {x}_2=\dot{x} \\ {\dot{x}}_1=x_2 \\ {\dot{x}}_2=\ddot{x}=\frac{1}{m}u-\frac{B}{m}{x}_2-\frac{k}{m}{x}_1 \end{gathered}$$
这时我们可以列出它们前后的状态矩阵的关系：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -\frac{k}{m}& -\frac{B}{m}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ \frac{1}{m}\end{array}\right]u$$
而在一个系统中通常不单单只有状态量，还有观测量。这时假设我们观测得到的值没有误差，即$$\begin{gathered} Z_1=x=x_1(位置) \\ {Z}_2=\dot{x}=x_2(速度) \end{gathered}$$
可以得测量矩阵方程：
$$\left[\begin{array}{c}{Z}_1\\ Z_2\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$
通过提炼上面的状态矩阵方程和测量矩阵方程我们可以得到：
$$\begin{array}{rl}{\dot{X}}_{(t)}& =A{X}_{(t)}+B{u}_{(t)}\\ Z_{(t)}& =H{X}_{(t)}\end{array}$$
离散化可得：
$$\begin{array}{rl}{X}_k& =A{X}_{k-1}+B{u}_{k-1}\\ Z_k& =H{X}_k\end{array}$$
同时一个系统在变化时会有过程噪声${\omega }_k$，测量时会有测量噪声${\nu }_k$（噪声可理解为误差）
最终我们可以得到一个较通用的离散化状态空间方程：
$$\begin{array}{rl}{X}_k& =A{X}_{k-1}+B{u}_{k-1}+{\omega }_k\\ Z_k& =H{X}_k+{\nu }_k\end{array}$$

噪声的协方差矩阵

对于不确定的噪声，我们一般视它服从期望为0的正态分布。
那么这个噪声的协方差矩阵是多少呢。
假设现在一个噪声$\omega$且$P(\omega )\sim (0,Q)$，其中$Q$就是这个噪声的协方差矩阵。
可知$D(\omega )=E({\omega }^2)-E(\omega {)}^2=E({\omega }^2)$
即$Q=E[\omega {\omega }^T]$

字符定义

$X_k$为系统第k次所得状态真实值
${\hat{X}}_k^{-}$为系统第k次所得状态先验估计值（即模型计算出来的，未进行数据融合的值）
${\hat{X}}_k$为系统第k次所得状态后验估计值（即进行数据融合优化过的值）
$u_k$为对系统输入的控制量
$Z_k$为系统第k次测量值
$A$为状态矩阵，$B$为控制矩阵，$H$为测量矩阵
${\omega }_k$为过程噪声且$P(\omega )\sim (0,Q)$，$Q$为过程噪声协方差矩阵
${\nu }_k$为测量噪声$P(\nu )\sim (0,R)$，$R$为测量噪声协方差矩阵
$e_k$为测量噪声$P(e)\sim (0,P)$，$P$为误差协方差矩阵

推导目标

由前置知识我们知道要描述一个系统可以用状态空间方程
$$\begin{array}{rl}{X}_k& =A{X}_{k-1}+B{u}_{k-1}+{\omega }_{k-1}\\ Z_k& =H{X}_k+{\nu }_k\end{array}$$
因为噪声是不测的，所以我们可以掌握的是
$$\begin{array}{rl}{\hat{X}}_k^{-}& =A{\hat{X}}_{k-1}+B{u}_{k-1}\\ {\hat{X}}_k^{-}& =H^{-1}{Z}_k(即Z_k=H{\hat{X}}_k^{-})\end{array}$$
其中第一条为我们的建立的模型所预测的（未优化），第二条为测量所得，两个数据都存在误差（即噪声），我们可以前置知识中的数据融合，来将这两个数据融合成一个误差更小的数据，即：
$${\hat{X}}_k={\hat{X}}_k^{-}+G(H^{-1}{Z}_k-{\hat{X}}_k^{-})$$
令$G=K_{k}H$得：${\hat{X}}_k={\hat{X}}_k^{-}+K_k(Z_k-H{\hat{X}}_k^{-})$
可知：
$$\begin{gathered} K_k\in [0,H^{-1}] \\ 当K_k=0时，{\hat{X}}_k={\hat{X}}_k^{-} \\ 当K_k=H^{-1}时，{\hat{X}}_k=H^{-1}{Z}_k \end{gathered}$$
我们的目标就是选择合适的$K_k$让我们优化后的数据${\hat{X}}_k$接近真实值$X_k$，使误差协方差矩阵的迹最小。

卡尔曼增益$K_k$

设误差$e_k=X_k-{\hat{X}}_k$，且误差服从正态分布$P(e_k)\sim (0,P)$
先推导$e_k$
$$\begin{array}{rl}{e}_k& =X_k-{\hat{X}}_k\\ & =X_k-({\hat{X}}_k^{-}+K_k(Z_k-H{\hat{X}}_k^{-}))\\ & =X_k-{\hat{X}}_k^{-}-K_k{Z}_k+H{\hat{X}}_k^{-}\\ & =X_k-{\hat{X}}_k^{-}-K_{k}H{X}_k-K_k{\nu }_k+H{\hat{X}}_k^{-}\\ & =(I-K_{k}H)(X_k-{\hat{X}}_k^{-})-K_k{\nu }_k\end{array}$$
所以误差协方差矩阵为：
$$\begin{array}{rl}{P}_k& =E[e_k{e}_k^T]\\ & =E[(X_k-{\hat{X}}_k)(X_k-{\hat{X}}_k{)}^T]\\ & =E[((I-K_{k}H)(X_k-{\hat{X}}_k^{-})-K_k{\nu }_k\left)\right((I-K_{k}H)(X_k-{\hat{X}}_k^{-})-K_k{\nu }_k{)}^T]\end{array}$$
结合线代和概率论知识：
$$\begin{gathered} (AB{)}^T=B^T{A}^T \\ (A+B{)}^T=A^T+B^T \\ E(e_k^{-}{\nu }_k^T)=0 \end{gathered}$$
最终可得：
$$\begin{array}{rl}{P}_k& =E[((I-K_{k}H)(X_k-{\hat{X}}_k^{-})-K_k{\nu }_k\left)\right((I-K_{k}H)(X_k-{\hat{X}}_k^{-})-K_k{\nu }_k{)}^T]\\ & =(I-K_{k}H)E(e_k^{-}{e}_k^{-T})(I-K_{k}H{)}^T+K_{k}E({\nu }_k{\nu }_k^T)K_k^T\\ & =(P_k^{-}-K_{k}H{P}_k^{-})(I^T-H^T{K}_k^T)+K_k\\ & =P_k^{-}-K_{k}H{P}_k^{-}-P_k^{-}{H}^T{K}_k^T+K_{k}H{P}_k^{-}{H}^T{K}_k^T+K_{k}R{K}_k^T\end{array}$$
可由$\frac{dtr(AB)}{dA}=B^T$得：
$$\frac{dtr(P_k)}{d{K}_k}=0-2(H{P}_k^{-}{)}^T+2K_k{P}_k^{-}{H}^T+2K_{k}R=0$$
解得$$K_k=\frac{P_k^{-}{H}^T}{H{P}_k^{-}{H}^T+R}$$
$$\begin{gathered} K_k\in [0,H^{-1}] \\ 我们可以知道，当R\to \infty 时，K_k=0，{\hat{X}}_k={\hat{X}}_k^{-} \\ 当R\to 0时，K_k=H^{-1}，{\hat{X}}_k=H^{-1}{Z}_k \end{gathered}$$

误差协方差矩阵$P_k$

我们现在已经得到卡尔曼滤波的三条公式，分别为：
$$\begin{array}{rl}先验估计值{\hat{X}}_k^{-}& =A{\hat{X}}_{k-1}+B{u}_{k-1}\\ 后验估计值{\hat{X}}_k& ={\hat{X}}_k^{-}+K_k(Z_k-H{\hat{X}}_k^{-})\\ 卡尔曼增益K_k& =\frac{P_k^{-}{H}^T}{H{P}_k^{-}{H}^T+R}\end{array}$$
可以发现其中还差一个$P_k^{-}$，这节我们就是来求这个。
先简化一下$e_k^{-}$:
$$\begin{array}{rl}{e}_k^{-}& =X_k-{\hat{X}}_k^{-}\\ & =(A{X}_{k-1}+B{u}_{k-1}+{\omega }_{k-1})-(A{\hat{X}}_{k-1}+B{u}_{k-1})\\ & =A{e}_{k-1}+{\omega }_{k-1}\end{array}$$
所以：
$$\begin{array}{rl}{P}_k^{-}& =E[e_k^{-}{e}_k^{-T}]\\ & =E[(A{e}_{k-1}+{\omega }_{k-1})(A{e}_{k-1}+{\omega }_{k-1}{)}^T]\\ & =E[(A{e}_{k-1}+{\omega }_{k-1})(e_{k-1}^T{A}^T+{\omega }_{k-1}^T)]\\ & =AE[e_{k-1}{e}_{k-1}^T]A^T+E[{\omega }_{k-1}{\omega }_{k-1}^T]\\ & =A{P}_{k-1}{A}^T+Q\end{array}$$
其中$P_{k-1}$可由之前的公式继续推得：
$$\begin{array}{rl}{P}_k& =P_k^{-}-K_{k}H{P}_k^{-}-P_k^{-}{H}^T{K}_k^T+K_{k}H{P}_k^{-}{H}^T{K}_k^T+K_{k}R{K}_k^T\\ & =P_k^{-}-K_{k}H{P}_k^{-}-P_k^{-}{H}^T{K}_k^T+K_k(H{P}_k^{-}{H}^T+R)K_k^T\\ & =P_k^{-}-K_{k}H{P}_k^{-}-P_k^{-}{H}^T{K}_k^T+\frac{P_k^{-}{H}^T}{H{P}_k^{-}{H}^T+R}(H{P}_k^{-}{H}^T+R)K_k^T\\ & =P_k^{-}-K_{k}H{P}_k^{-}\\ & =(I-K_{k}H)P_k^{-}\end{array}$$
到此所有的公式就都推导出来了。

卡尔曼滤波器使用说明

预测	校正
先验估计${\hat{X}}_k^{-}=A{\hat{X}}_{k-1}+B{u}_{k-1}$	卡尔曼增益$K_k=\frac{P_k^{-}{H}^T}{H{P}_k^{-}{H}^T+R}$
先验误差协方差$P_k^{-}=A{P}_{k-1}{A}^T+Q$	后验估计${\hat{X}}_k={\hat{X}}_k^{-}+K_k(Z_k-H{\hat{X}}_k^{-})$
	更新误差协方差$P_k=(I-K_{k}H)P_k^{-}$

${\hat{X}}_k^{-}$为状态先验估计值（即模型计算出来的，未进行数据融合的值）
${\hat{X}}_k$为状态后验估计值（即进行数据融合优化过的值）
$u_k$为对系统输入的控制量
$Z_k$为测量值
$A$为状态矩阵，$B$为控制矩阵，$H$为测量矩阵
$Q$为过程噪声协方差矩阵
$R$为测量噪声协方差矩阵
$P$为误差协方差矩阵
其中，$A,B,H$与估计模型和测量方式有关，是不可变的，但可以确定。而$Q,R$是噪声，不可确定，也不可变，只能大概判断给出。而剩下的都是可变的。
在卡尔曼滤波器的使用过程中，我们只需要确定的是后验估计${\hat{X}}_1$和后验误差协方差$P_1$，然后整个模型会随着测量值$Z_k$和控制量$u_k$的输入来调整自身使其最佳。
$$\begin{array}{rl}step1& 计算卡尔曼系数K_k=\frac{e_{ES{T}_{k-1}}}{e_{ES{T}_{k-1}}+e_{ME{A}_k}}\\ step2& 计算估计值{\hat{X}}_k={\hat{X}}_{k-1}+K_k\times (Z_k-{\hat{X}}_{k-1})\\ step3& 更新估计误差e_{ES{T}_k}=(1-K_k)\times e_{ES{T}_{k-1}}\end{array}$$
大家也看出一阶卡尔曼就是它的简化，只有校正部分，但在调整参数上两者出现的反应差不多，大家可以自行调整测试看看。

扩展卡尔曼

我还不会，等我学会了有空就继续写。