数制与编码

• 编码：用少量简单的基本符号，对大量复杂多样信号进行一定规律的组合表示

数值数据的编码表示

• 数值数据的表示方法：直接用二进制表示：定点或浮点表示方法； BCD码…

• 数值数据在计算机内部编码表示的数称为机器数。机器数真正的值称为机器数的真值

校验码

• 校验位：在有效信息数据代码之外，再扩充几位。增加的部分称为冗余位或校验位
• 码字：若干位二进制代码组成的一个字
• 码制：包含若干种码字的集合 (ASCII码、BCD码…)
• 距离：在一种码制中将两个码字逐位比较，具有不同代码的位的个数叫做这两个码字间的“距离” (例如在8421BCD码中，0000和1001的距离为2)
• 码距：将一种码制中各码字间的最小距离称为“码距”(例如在8421BCD码中，码距为1。如果发生1位传输错误，则无法查出错误)

合理增大码距，能提高发现错误的能力，但表示一定数量的合法码所使用的二进制位数要变多，增加了电子线路的复杂性和数据存储、数据传送的数量

• $k$ 位码有 $2^k$ 个编码状态，全用于表示合法码，则任何一位出错 , 均会变成另一个合法码，不具有检错能力
• 从一个合法码变成另一个合法码，至少要改变几位码的值，称为最小码距 (码距 )，码距和编码方案将决定其检错纠能力

校验过程：

1. 编码过程：对原始数据进行编码，产生一个校验位，把校验位附加到原始数据中
2. 将包含原始数据以及校验信息的码字进行传送
3. 对接收到的码字进行译码，检查收到的码字，发现 / 改正错误

海明校验码：用于并行数据传送中

奇偶校验码：用于并行数据传送中

实现原理：使码距由1增加到2。若编码中有1位二进制数出错了，出错的编码就成为非法编码，就可以知道出现了错误。在原有的编码之上再增加1位校验位，原编码 $k$ 位，形成新的编码为 $k+1$ 位。增加的方法有2种：

• 奇校验：增加位的0或1，保证整个编码中1的个数为奇数
• 偶校验：增加位的0或1，保证整个编码中1的个数为偶数

实现原理：假设将数据 $D=d_{n-1}{d}_{n-2}...d_1{d}_0$ 从源部件传送至目的部件。在目的部件接收到的数据为:
$$D^{\prime }=d_{n-1}^{\prime }{d}_{n-2}^{\prime }...d_1^{\prime }{d}_0^{\prime }$$

1. 在源部件求出奇（偶）校验位 $P$
   若采用奇校验，则 $P=d_{n-1}\oplus d_{n-2}\oplus ...\oplus d_1\oplus d_0\oplus 1$
   若采用偶校验，则 $P=d_{n-1}\oplus d_{n-2}\oplus ...\oplus d_1\oplus d_0$
2. 在目的部件求 $P^{\prime }=d_{n-1}^{\prime }\oplus d_{n-2}^{\prime }\oplus ...\oplus d_1^{\prime }\oplus d_0^{\prime }$
3. 产生最终的出错指示位 $P^{\ast }$
   假设 $P$ 在目的部件接收到的值为 $P^{\prime \prime }$
   若采用奇校验，则 $P^{\ast }=P^{\prime }\oplus P^{\prime \prime }\oplus 1$
   若采用偶校验，则 $P^{\ast }=P^{\prime }\oplus P^{\prime \prime }$
   ① 若 $P^{\ast }=1$，则表示目的部件接收的数据有奇数位错
   ② 若 $P^{\ast }=0$，则表示目的部件接收的数据正确或有偶数位错

• 特点：在奇偶校验码中，若两个码字中有奇数位不同，则它们的校验位就不同；若有偶数位不同，则虽校验位相同，但至少有两位数据位不同。因而任意两个码字之间至少有两位不同，所以码距 $d=2$。所以，只能发现奇数位出错，不能发现偶数位出错，而且不能确定发生错误的位置，不具纠错能力
• 优点：开销小，常被用于存储器读写检查或按字节传输过程中的数据校验。因为一字节长的代码发生错误时，1位出错的概率较大，两位以上出错则很少，所以奇偶校验码用于校验一字节长的代码是有效的

循环冗余校验码：用于串行数据传送中

CRC（Cyclical Redundancy Check）校验码一般是指 $k$ 位信息之后拼接 $r$ 位校验码

CRC码的编码方法

CRC整个编码长度为 $n=k+r$ 位，故CRC码又叫 $(n，k)$ 码。其编码方法如下：

1. 假设被传送的 $k$ 位二进制信息位用 $C(x)$ 表示, 系统选定的生成多项式用 $G(X)$表示，将 $C(x)$ 左移 $G(X)$ 的最高次幂(即等于需要添加的校验位的位数 $r$)，写作 $C(x)\cdot 2^r$
2. 将 $C(x)\cdot 2^r$ 除以生成多项式 $G(X)$ ，所得商用 $Q(x)$ 表示，余数用 $R(x)$ 表示。则有：
   $$C(x)\cdot 2^r-R(x)=Q(x)\cdot G(x)$$

CRC编码采用的是按位加、减法，即不考虑进位与借位，运算规则为： $0\pm 0=0，0\pm 1=1，1\pm 0=1，1\pm 1=0$。因此
$$C(x)\cdot 2^r+R(x)=Q(x)\cdot G(x)$$

上式中，等式左边即为所求的 $n$ 位CRC码，其中余数表达式 $R(x)$ 就是校验位( $r$ 位)。且等式两边都是 $G(x)$ 的倍数

发送信息时将等式左边生成的 $n$ 位CRC码送给对方。当接收方接到 $n$ 位编码后，同样除以 $G(x)$，如果传输正确则余数为0，否则，可以根据余数的数值确定是哪位数据出错

例
有一个（7,4）码，已确定生成多项式为： $G(X)=X^3+X+1=1011$。被传输的信息 $C(x)=1001$，求 $C(x)$ 的CRC码
解
$$C(x)\cdot 2^r=1001\times 2^3=1001000$$

因此$R(x)=110$，CRC码为 $1001110$

列出CRC码的查错表

如果循环码有一位出错，用 $G(x)$ 作模2除将得到一个不为0的余数。如果对余数补1个0继续除下去，将发现一个现象： 各次余数将按上述表顺序循环

• 例如，第 $A_1$ 位出错，余数将为 001 ，补0后再除，第二次余数为 010 ，以后依次为 100 ，011,…101 ，001… 反复循环
• 如果在求出余数不为0后，一边对余数补0继续做模2除， 同时让被检错的校验码字循环左移
• 由表中可见，当出现余数（ 101 ）时，出错位也移到 $A_7$ 位 置，可以 通过异或门将它纠正后，在下一次移位时送回 $A_7$ 。 继续移满一个循环（对 7、4码共移 7次），就得到一个纠正后的码字。当位数增多时循环校验能有效地降低硬件代价

生成多项式 $G(x)$ 的确定

• 为了得到 $r$ 位余数，$G(x)$ 必须是 $r+1$ 位
• 任何一位发生错误都应使余数不为0
• 不同位发生错误应使余数不同
• 余数继续模2 除，应使余数循环

定点数的表示和运算

定点数的表示

• 定点数：在计算机中，小数点位置固定不变的数。定点表示即为约定小数点的位置固定在数的最左边或最右边。小数点不占用存储位

定点小数 (原码、反码、补码)

• 定点小数：小数点隐含在数的最左边
  $$X=X_0{X}_{-1}{X}_{-2}\dots X_{-(n-1)}$$ $n$ 位字长 ($1$ 位符号位，$n-1$ 位数值位)，下标 $i$ 表示该位的权为 $2^i$

---

原码

• 原码是符号位加数的绝对值
• 原码零有两个编码， $+0$ 和 $-0$ 的编码不同
• 原码难以用于加减运算，但乘除方便

例
$$X=0.1011\to [X{]}_{原}=01011$$$$X=-0.1011\to [X{]}_{原}=11011$$$$X=0.0000\to [X{]}_{原}=00000或10000$$

---

反码

---

补码

• 补码表示为： 2 $\times$ 符号位 $+$ 数的真值，最高一位是符号位
• 补码零只有一个编码，故能表示 $-1$ (即 $10000$)
• 补码能很好地用于加减乘除运算

例
$$X=0.1011\to [X{]}_{补}=01011$$$$X=-0.1011\to [X{]}_{补}=100000-01011=10101$$$$X=0.0000\to [X{]}_{补}=00000$$

得到一个数补码表示的简便办法

• 当 $X<0$ 时，$[X{]}_{补}$ 的符号位取 $1$，将 $X$ 的各数值位取反,再在最低位加 $1$，以得到 $[X{]}_{补}$ 的各数值位上的值 (i.e., $[X{]}_{补}=[X{]}_{反}+2^{-(n-1)}$)

$[X{]}_{原}$与$[X{]}_{补}$的相互转换简便方法

• 从$[X{]}_{原}$求$[X{]}_{补}$时，对正数或零，有$[X{]}_{补}=[X{]}_{原}$，对负数则符号位不变，各数值位变反后再在最低位执行加 $1$ 操作
  (这种方法也可以表述为：除符号位外，从最右边的第 $1$ 个 $1$ 开始，左边的位依次取反)
  由$[X{]}_{补}$求 $[X{]}_{原}$时，对负数仍是符号位不变，各数值位变反后再在最低位执行加 $1$ 操作

已知 $[y{]}_{补}$，求 $[-y{]}_{补}$：
将 $[y{]}_{补}$ 连同符号位在内，每位取反，末位加1，得到 $[-y{]}_{补}$
(即 $[-y{]}_{补}=2-2^{-(n-1)}-[y{]}_{补}+2^{-(n-1)}=2-[y{]}_{补}$。可以分 $y\ge 0$ 和 $y<0$ 进行证明)

整数

整数形式：小数点隐含在数的最右边

$1$ 位符号位，$n-1$ 位数值位

原码

$X$ 为真值

反码

补码

整数的移码表示 (用于浮点数阶码)

设 $X$ 为真值，若机器字长为 $n$ 位，则：
$$[X{]}_{移}=2^{n-1}+X-2^{n-1}\le X\le 2^{n-1}-1$$

$$[X{]}_{移}=2^{n-1}+X=2^n+2^{n-1}+X=2^{n-1}+[X{]}_{补}$$

因此，同一个整数的移码与补码仅符号位相反

定点数的运算

定点数的移位运算

算术移位：移位的对象是数值型数据，在移位后会发生数值大小的变化

• 对于二进制数，左移，绝对值扩大；右移，绝对值缩小
• 算术移位规则：左移与逻辑移位相同，右移带符号位移位

逻辑移位：逻辑左移、逻辑右移、循环左移和循环右移等。逻辑移位只是使数码位置发生变化，没有正、负性质，也没有数值大小问题

算术移位和逻辑移位的区别：
算术移位：带符号数移位
逻辑移位：无符号数移位

补码定点数的加/减运算

$n$ 位字长

加法：

• 整数
  $[X+Y{]}_{补}=[X{]}_{补}+[Y{]}_{补}（mod{2}^n）$
• 小数
  $[X+Y{]}_{补}=[X{]}_{补}+[Y{]}_{补}（mod2）$

减法

• 整数
  $[X－Y{]}_{补}=[X+（-Y）{]}_{补}=[X{]}_{补}+[-Y{]}_{补}（mod{2}^n）$
• 小数
  $[X－Y{]}_{补}=[X+（-Y）{]}_{补}=[X{]}_{补}+[-Y{]}_{补}（mod2）$

补码运算的特点：

1. 无需符号判定，数值位连同符号位一起相加，符号位产生的进位自然丢掉
2. $[-Y{]}_{补}=$ 对 $[Y{]}_{补}$ 逐位取反，再在最低位加 $1$

溢出概念和判别方法

1. 单符号位： 当任意两个有符号数相加时，设 $C_f$ 为最高数值位的进位， $C_s$ 为符号位的进位，若 $C_f=C_s$，运算结果正确；若 $C_f\ne C_s$ ，则产生溢出
   溢出条件：$OV=C_s\oplus C_f$
2. 双符号位：变形补码，第一符号位$S_{f_1}$，第二符号位$S_{f_2}$，正数的双符号位为 $00$，负数的双符号位为 $11$。符号位参与运算，当结果的两个符号位不相同时为溢出
   溢出条件：$OV=S_{f_1}\oplus S_{f_2}$
   运算结果为 $01$ （正溢）或 $10$（负溢），最高符号位 $S_{f_1}$ 代表其真正的符号

例.
$X=0.1011,[X{]}_{补}=001011$
$Y=-0.0101,[Y{]}_{补}=111011,[-Y{]}_{补}=000101$

定点数的乘法运算

原码一位乘法

两个原码数相乘，其乘积的符号为相乘两数的异或值，数值为两数绝对值之积

$$[X\cdot Y{]}_{原}=[X{]}_{原}[Y{]}_{原}=(X_0\oplus Y_0)|(|X|\cdot |Y|)$$

例.
$X=0.1101$ ，$Y=0.1011$，求 $X\cdot Y$

如果直接使用手工运算的计算方法的话，硬件电路会变得比较复杂(要实现四个数的相加)

解决方法：

• 将被乘数与乘数的最低位相乘，得到的结果称为部分积。部分积初始为0
• 算出新的部分积，与原来的部分积相加，然后右移1位。同时被乘数也要右移1位
• 不断重复上述步骤，最后得到的部分积的和即为最后的乘积
• 最后再加上符号位得到最后的结果

硬件：设置3个寄存器(具有逻辑右移功能)：

1. $A$：存放部分积累加和、乘积高位
2. $B$：存放被乘数
3. $C$：存放乘数、乘积低位
4. 一个全加器，一个计数器 $C_d$ (确定循环次数)

设置初值：
$$A=00.0000,B=|X|=00.1101,C=|Y|=.1011$$

如上图所示，部分积 $A$ 初始为 0，用乘数 $C$ 的最低位乘上乘数 $B$ 并加上原有部分积后得到新的部分积 $1101$，接着 $A$ 和 $C$ 同时右移1位，$A$ 的最低位保存到了乘数 $C$ 的最高位中，$C$ 的最低位已经没有用了，可以直接丢弃。
接着继续重复刚才的步骤，用乘数 $C$ 的最低位乘上乘数 $B$ 并加上原有部分积后得到新的部分积 $10011$,…
当重复上述步骤 $C_d=4$ 次(乘数 $C$ 的位数)之后，乘法结束

定点补码一位乘法

补码一位乘法：乘法直接用补码进行，以减少转换次数

以定点小数为例：
$$\begin{gathered} [X{]}_{补}=X_0.X_1{X}_2...X_n \\ [Y{]}_{补}=Y_0.Y_1{Y}_2...Y_n \end{gathered}$$( 公式中的 $.$ 表示小数点的位置)
***下面进行推导：
$$\begin{array}{rl}\because [X{]}_{补}& =2X_0+X\\ \therefore X& =[X{]}_{补}-2X_0\\ & =X_0{X}_1...X_n-2X_0\\ & =X_0+X_1...X_n-2X_0\\ & =-X_0+0.X_1...X_n\end{array}$$

上面推导出的公式可以将符号位与数值位分开

接着上面的结论推导：
$$\begin{array}{rl}[X\cdot Y{]}_{补}& =[X\cdot (-Y_0+0.Y_1...Y_n){]}_{补}\\ & =[-X\cdot Y_0{]}_{补}+[X\cdot 0.Y_1...Y_n{]}_{补}\\ & =[-X{]}_{补}\cdot Y_0+[X{]}_{补}\cdot (0.Y_1...Y_n)\\ & (0.Y_1...Y_n可以看作Y_1\cdot 2^{-1}+...+Y_n\cdot 2^{-n})\\ & =[X{]}_{补}\cdot (0.Y_1...Y_n)-[X{]}_{补}\cdot Y_0\\ & =[X{]}_{补}(-Y_0+2^{-1}{Y}_1+...+2^{-n}{Y}_n)\\ & =[X{]}_{补}(-Y_0+(Y_1-2^{-1}{Y}_1)+...+(2^{-(n-1)}{Y}_n-2^{-n}{Y}_n))\\ & =[X{]}_{补}((Y_1-Y_0)+2^{-1}(Y_2-Y_1)+...+2^{-n}(Y_{n+1}-Y_n))\\ & (Y_{n+1}=0,Y_0为符号位)\end{array}$$

布斯（Booth）算法：过程类似于原码1位乘法。用部分积和移位进行计算。用相邻两位乘数比较的结果决定给部分积加 $[X{]}_{补}、[-X{]}_{补}$ 或 $0$

1/2 表示右移1位

1. 部分积 $A$、被乘数 $B$ 取双符号位，符号位参加运算
2. 乘数 $C$ 取单符号位，符号参加移位，以决定最后是否修正
3. $C$ 末位设置附加位 $C_{n+1}$，初值为 $0$，$C_n{C}_{n+1}$组成判断位，决定运算操作，作 $n$ 步循环
4. 第 $n+1$ 步由（$Y_1-Y_0$）决定,仅修正，不移位

例
$X=-0.1101,Y=0.1011$，求$[X\cdot Y{]}_{补}$
解
初值：$A=00.0000,B=[X{]}_{补}=11.0011,-B=[-X{]}_{补}=00.1101,C=[Y{]}_{补}=0.10110$

注意：上面的移位为算术移位

浮点数的表示和运算

浮点数的表示

• 浮点数是指小数点位置可随比例因子的不同而浮动的数据，通常以下式表示：
  $$N=M\times R^E$$其中，$N$ 为浮点数，$M$ 为尾数，$E$ 为阶码，$R$ 为 “阶的基数 (底)”
• 在一台计算机中，所有数据的 $R$ 都是相同的，故无需在每个数据将 $R$ 表示出来。浮点数的一般机器格式为：
  
  • $M_s$ 是尾数的符号位，设置在最高位 (数符表示数的正负)
  • $E$ 为阶码，有 $n+1$ 位，一般为定点整数，其中有一位符号位 $E_J$，设置在 $E$ 的最高位上，用来表正阶或负阶 (阶符表示数的大小)。阶码用补码或移码表示。其位数决定数值范围
  • $M$ 为尾数，有 $m$ 位，为一个定点小数。尾数用原码或补码表示。其位数决定数的精度

---

例
设某机器用32位表示一个实数，阶码部分8位（含1位阶符），用定点整数补码表示；尾数部分24位（含数符1位），用规格化定点小数补码表示，基数为2。给出 $X=256.5$ 和 $Y=-256.5$ 的浮点表示形式
解

浮点数规格化

为了保证数据精度，尾数通常用规格化形式表示：

• 当 $R＝2$，且尾数值不为 $0$ 时，其绝对值大于或等于 $0.5$
• 对非规格化浮点数，通过将尾数左移或右移，并修改阶码值使之满足规格化要求

增加尾数位数也可以提高精度，但数值范围减小 (阶码位数减少了)

尾数为原码表示时，无论正负应满足

• 小数点后的第一位数一定要为1

尾数用补码表示时，无论正负应满足

• 小数最高位应与数符位相反
  正数 ($\frac{1}{2}\le M<1$)：$0.1x...x$
  负数 ($-1\le M<-\frac{1}{2}$)：$1.0x...x$

注意：
$S=-\frac{1}{2}=-0.100,[S{]}_{原}=1.100,[S{]}_{补}=1.100$，因此 $[-\frac{1}{2}{]}_{补}$ 不是规格化数
$S=-1,[S{]}_{补}=1.00...0$， 因此 $[-1{]}_{补}$ 是规格化数

浮点数的溢出判断

根据规格化后的阶码判断：

• 上溢——浮点数阶码大于机器最大阶码—中断
• 下溢——浮点数阶码小于机器最小阶码—按机器零处理

假如不考虑规格化：

若考虑规格化，则

• 最小正数：$2^{-1}\times 2^{-(2^m-1)}$
• 最大负数：$-2^{-1}\times 2^{-(2^m-1)}$

IEEE754 标准

1. 单精度浮点数（32位），阶码8位，尾数24位（内含1位符号位）
2. 双精度浮点数（64位），阶码11位，尾数53位（内含1位符号位）

• 由于IEEE754标准约定小数点左边的位恒为1(这个 $1$ 被省去)，从而实际使得尾数的有效值变为 $1.M$
• 尾数 $m$ 用原码表示。其规格化形式应调整阶码使其尾数整数位为 $1$ 且与小数点一起隐含掉
• 阶码 $E$ 是一个用移码表示的无符号整数：$n$ 位阶码，偏移量为 ( $2^{n-1}-1$ )，即 $127$ 或 $1023$。因此，指数项 $e=E-(2^{n-1}-1)$

阶码使用的移码偏移量为什么不用 128 ？
因为若用128，则最大阶127对应的编码127+128=255，而255(全1)要用来表示一些特殊值

IEEE754 标准中的规范化浮点数：

• 阶码为非全0非全1的数是正常的规格化浮点数。即：阶码范围在 $1$~$254$ (单精度)和 $1$~$2046$ (双精度)的数是一个正常的规格化数
  根据IEEE754 的定义，可知其阶码的真值范围：
  $-126$~$+127$（单精度）
  $-1022$~$+1023$（双精度）

---

• **全0阶码全0尾数：表示 $+0/-0$
• 全0阶码非0尾数：阶码域为全0时所表示的数是非规格化形式，此时尾数不含第一位隐含的1，单精度或双精度数的真值：
  $(-1{)}^s\times 0.M\times 2^{-126}$ 或 $(-1{)}^s\times 0.M\times 2^{-1022}$
  阶码值为 $1-偏移量（127或1023）$，提供了一种从非规格化值平滑转换到规格化值的方法
• 全1阶码全0尾数：表示$+\infty /-\infty$
• 全1阶码非0尾数：$NaN$ (Not a Number 非数，无定义数)

---

单精度浮点数最大表示范围：
$$\pm (1.1111...1)\times 2^{127}=\pm (2-2^{-23})\times 2^{127}\approx \pm 3.40282\times 10^{38}$$

单精度浮点数可以表示接近于 0 的最小的绝对值：
$$\pm (1.000...00)\times 2^{-126}=\pm 1\times 2^{-126}\approx \pm 1.175\times 10^{-38}$$

例
将十进制数 $178.125$ 表示成微机中的单精度浮点数
解:

浮点数的加/减运算

两数首先均为规格化数，进行规格化浮点数的加减运算需经过5步完成：

1. 对阶操作：低阶向高阶补齐，使阶码相等
   阶码较小的数将阶码增大，尾数减小 (阶码每增大1，尾数就进行1位右移。尾数为原码时，尾数右移时，符号位不动，最高数值位补0；尾数为补码时，尾数右移时，符号也移位，最高位补符号位。)

2. 尾数运算：阶码对齐后直接对尾数运算

3. 结果规格化：对运算结果进行规格化处理。如尾数溢出则需右规(尾数向右移位直到它为规格化的数)；如不是，规格化时应左规

4. 舍入操作：在对阶和右规过程中，可能出现尾数末位丢失引起误差，需考虑舍入。丢失位进行0舍1入或恒置1处理。常用“0”舍“1”入法：当移掉的部分最高位为1时，在尾数的末尾加1，如果加1后又使得尾数溢出，则要再进行一次右规

5. 判断溢出：判断阶码是否溢出，下溢则将运算结果置0（机器0），上溢则设置溢出标志

例
$x=0.1101\times 2^{01},y=(–0.1010)\times 2^{11}$，求 $x+y$
解
先将两数的阶码和尾数都用双符号位的补码表示(阶码和尾数之间用分号隔开)
$$[x{]}_{补}=00,01;00.1101,[y{]}_{补}=00,11;11.0110$$

1. 对阶
   ①求阶差：$[\Delta j{]}_{补}=[j_x{]}_{补}–[j_y{]}_{补}=00,01+11,01=11,10$。因此阶差为 $-2$ ，$\therefore S_x\to 2,j_x+2$
   ②对阶：$[x{]}_{补}^{\prime }=00,11;00.0011$
2. 尾数求和
   $[S_x{]}_{补}^{\prime }+[S_y{]}_{补}=00.0011+11.0110=11.1001$
   $\therefore [x+y{]}_{补}=00,11;11.1001$
3. 规格化
   结果不是规格化数且结果没有溢出时应左规：尾数左移1位，阶码减1，直到结果规格化 (对于补码来说，规格化指数符与第一数位不同)
   $[x+y{]}_{补}=00,11;11.1001=00,10;11.0010$
   $\therefore x+y=-(0.1110{)}_2\times 2^2=-3.5$

例
$x=0.1101\times 2^{10},y=(0.1011)\times 2^{01}$，求 $x+y$
解
$$[x{]}_{补}=00,010;00.110100,[y{]}_{补}=00,001;00.101100$$

1. 对阶
   ①求阶差：$[\Delta j{]}_{补}=[j_x{]}_{补}–[j_y{]}_{补}=00,010+11,111=100,001$ (最高位的 $1$ 自然丢失)。因此阶差为 $+1$ ，$\therefore S_y\to 1,j_y+1$
   ②对阶：$[y{]}_{补}^{\prime }=00,010;00.010110$
2. 尾数求和
   $[S_x{]}_{补}^{\prime }+[S_y{]}_{补}=00.110100+00.010110=01.001010$
3. 规格化
   尾数溢出，因此右规 (尾数右移1位，阶码加1)
   $[x+y{]}_{补}=00,010;01.001010=00,011;00.100101$
   $\therefore x+y=(0.100101{)}_2\times 2^3=4.625$

例
$x=(-\frac{5}{8})\times 2^{-5},y=(\frac{7}{8})\times 2^{-4}$，求 $x-y$ (除阶符、数符外，阶码取3位，尾数取6位)
解
$$\begin{gathered} x=(-0.101000)\times 2^{-101},y=(0.111000)\times 2^{-100} \\ [x{]}_{补}=11,011;11.011000,[y{]}_{补}=11,100;00.111000 \end{gathered}$$

1. 对阶
   ①求阶差：$[\Delta j{]}_{补}=[j_x{]}_{补}–[j_y{]}_{补}=11,011+00,100=11,111$。因此阶差为 $-1$ ，$\therefore S_x\to 1,j_x+1$
   ②对阶：$[x{]}_{补}^{\prime }=11,100;11.101100$
2. 尾数求和
   $[S_x{]}_{补}^{\prime }+[-S_y{]}_{补}=11.101100+11.001000=110.110100$ (最高位的 $1$ 自然丢失)
3. 规格化
   尾数溢出，因此右规 (尾数右移1位，阶码加1)
   $[x-y{]}_{补}=11,100;10.110100=11,101;11.011010$
   $\therefore x-y=(-0.100110{)}_2\times 2^{-3}=(-\frac{19}{32})\times 2^{-3}$

算术逻辑单元 ALU

串行进位加法器

数电内容，就不具体写了

$$\begin{array}{rl}全加和S_i& =A_i\oplus B_i\oplus C_{i-1}\\ 全加进位C_i& =A_i{B}_i+B_i{C}_{i-1}+A_i{C}_{i-1}\\ & =A_i{B}_i+(A_i\oplus B_i)C_{i-1}\\ & =A_i{B}_i+(A_i+B_i)C_{i-1}\end{array}$$

特点：串行进位（又称行波进位）加法器，逻辑电路较简单，但最高位的加法运算，一定要等到所有低位的加法完成之后才能进行，低位的进位要逐步传递到高位，逐级产生进位，因此运算速度较慢

并行进位加法器

引进两个函数

• 进位产生函数：$G_i=A_i{B}_i$
• 进位传递函数：$P_i=A_i+B_i$

则 $C_i=G_i+P_i{C}_{i-1}$

因此，$n$ 位加法器的进位并行产生

• 并行进位加法器的运算速度很快，形成最高进位输出的延迟时间很短，但是以增加硬件逻辑线路为代价
• 对于长字长的加法器，往往将加法器分成若干组，在组内采用并行进位，组间采用串行进位或并行进位

先行进位加法器

单级先行进位：将 $n$ 位字长分为若干组，每组内采用并行进位方式，组与组之间则采用串行进位方式

ALU 电路

Arithmetic logical unit

利用集成电路技术可将若干位全加器、并行进位链、输入选择电路等部分集成在一块芯片上，称为多功能算术、逻辑运算部件 ALU

• ALU部件是运算器中的主要组成部分，又称为多功能函数发生器，主要用于完成各种算术运算和逻辑运算。ALU的算术运算部件包含加法器、减法器、乘法器、除法器、增量器（+1）、减量器（-1）、 BCD码运算器等组件
• ALU的主要工作是根据CPU的指令要求执行各种指定的运算，如加法、减法、乘法、除法、比较、逻辑、移位等操作

ALU 的核心是加法器。加法器大多采用“先行进位”方式

4位ALU部件 SN74181

• 用4片74181电路可组成16位ALU。如图所示，片内进位是快速的，但片间进位是逐片传递的，因此总的形成时间还比较长

---

• 如果把16位ALU中的每4位作为一组，用类似位间快速进位的方法来实现16位ALU（4片ALU组成），那么就能得到16位快速ALU：

利用16位并行进位链集成电路SN74182，产生芯片连接时所需要的并行进位信号，构成片内、片间均并行进位的ALU

• SN74182可以向SN74181提供片间并行进位信号，其芯片本身输出的G、P还可以支持更高一级的并行进位链，从而可构成更长位数的ALU
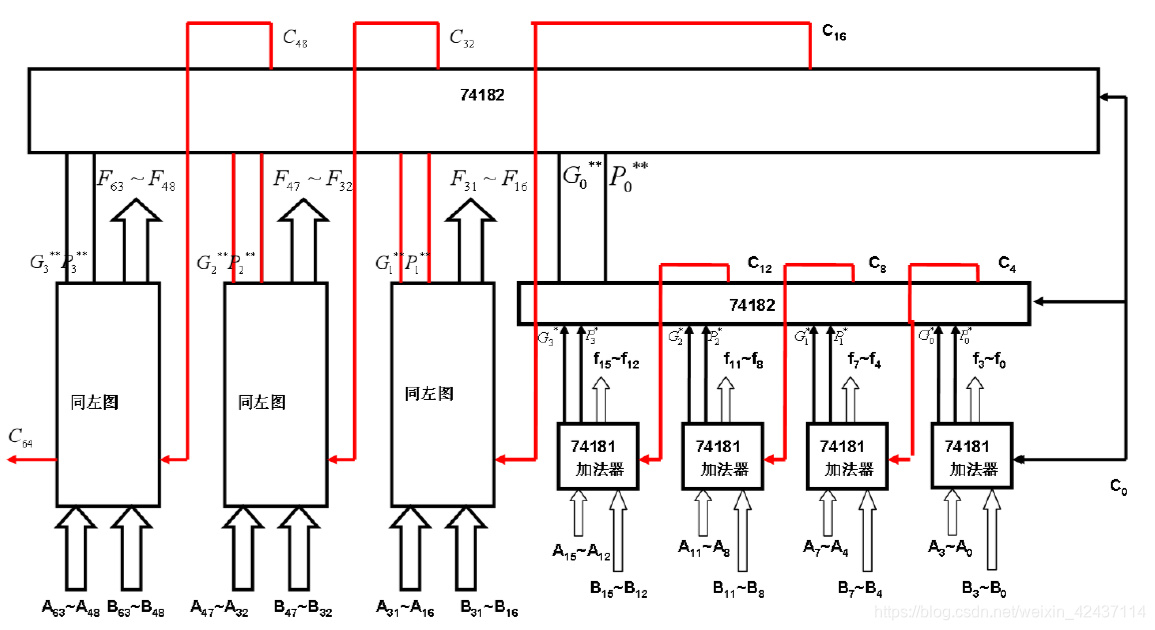
  例如，采用3片SN74182和8片SN74181可级连组成片内、片间均并行进位的32位ALU电路。5片SN74182和16片SN74181可级连组成片内、片间均并行进位的64位ALU电路(如下图所示)